• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Inducción matemática

Examinaremos una propiedad de los enteros positivos, que nos permitirá establecer algunas fórmulas matemáticas mediante una técnica llamada inducción.

Tratemos de expresar el subconjunto de los enteros positivos, Z⁺, mediante los símbolos de desigualdad > y >=.

Z⁺ = {x ∈ Z / x > 0} = {x ∈ Z / x >= 1}

Ahora, hagamos lo mismo con los números racionales positivos y los números reales positivos.

Q⁺ = {x ∈ Q / x > 0}
R⁺ = {x ∈ R / x > 0}

No podemos representar los números racionales y reales positivos con el signo >=. Q⁺ y R⁺ no contienen elementos mínimos. Por ejemplo, si q es un número racional positivo, q/2 es un número racional positivo más pequeo.

Principio del buen orden

Cualquier subconjunto no vacío de Z⁺ contiene un elemento mínimo.

Este principio es la base de una técnica de demostración conocida como inducción matemática. Esta técnica nos servirá con frecuencia para demostrar una proposición matemática general relacionada con los enteros positivos.

Principio de inducción matemática

Sea P(n) una proposición en la que aparece una o varias veces la variable n, que representa a un entero positivo.

a) Si P(1) es verdadera; y
b) siempre que P(k) sea verdadera (para algún k en Z⁺ particular, pero elegido al azar), entonces P(k+1) será verdadera;

entonces P(n) es verdadera para todo n ∈ Z⁺.

Sea P(n) una proposición con las condiciones a) y b), y sea F = {t ∈ Z⁺ / P(t) es falsa}.

Queremos mostrar que F = ∅.

Suponemos que F ≠ ∅.

Entonces, por el principio del buen orden, F tiene un elemento mínimo s.

Como P(1) es verdadera, s ≠ 1, por lo que s > 1, entonces s-1 ∈ Z+.

Como s-1 ∉ a F entonces P(s-1) es verdadera.

Así, por b), P((s-1) + 1) = P(s) es verdadera lo que contradice que s ∈ F.

La contradicción surge de la hipótesis F ≠ ∅. Por lo tanto, F = ∅.

La condición a) se conoce como la base de la inducción, y la parte b) se conoce como el paso inductivo.

En la condición a) la elección de 1 no es obligatoria. Lo único que se necesita es que la proposición P(n) sea verdadera para un primer elemento n₀ ∈ Z para que el proceso de inducción tenga un lugar de inicio. El entero n₀ podría ser 5 ó 1.

Imaginemos una fila de fichas de dominó, en la que el espacio entre fichas es siempre el mismo y es tal que si cualquier ficha (digamos la k-ésima) se empuja hacia la derecha, entonces golpeará la siguiente ((k+1) ésima).

La verdad de P(n₀) proporciona el empuje inicial y pone en movimiento el proceso de caída de las fichas.

Ejemplos:

1. Demostrar que para cualquier n ∈ Z⁺,
   
   

   Para n=1, P(1)=1 y 1(1+1)/2=1, entonces P(1) es verdadera.

   Supongamos que P es verdadera para n=k (para algún k ∈ Z⁺), queremos mostrar que la verdad de P(k) obliga a aceptar la verdad de P(k+1).

   Necesitamos mostrar que
   
   
   

   pues estamos suponiendo la verdad de P(k).

   Pero
   

   En consecuencia, por el principio de inducción, P(n) es verdadera para todo n ∈ Z⁺.

2. Demostrar que
   

P(1) = 2.1 - 1 = 1 = 1² ⇒ P(1) es verdadera.

Ahora supongamos que P(k) es verdadera.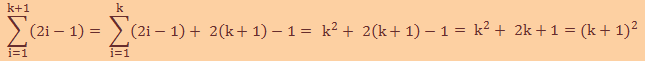



Con lo que P(k+1) es verdadera.

3. Demostrar que 4n < n² - 7 para todo n ≥ 6.

Denotemos con P(n) la proposición 4n < n² - 7.

n=6: P(6) = 4.6 = 24 y 6² - 7 = 36 - 7 = 29 ⇒ P(6) es verdadera.

Supongamos que P(k) es verdadera para k > 6, o sea que 4k < k² - 7

4k < k² - 7 ⇒ 4k + 4 < (k² - 7) + 4 < (k² - 7) + (2k + 1)

ya que 2k + 1 > 4 para k ≥ 6

⇒ 4(k + 1) < (k² + 2k + 1) - 7 = (k + 1)² - 7

Por lo tanto, por el principio de inducción, P(n) es verdadera para todo n ≥ 6.