Si cerráis la puerta a todos los errores, la verdad quedará afuera.
Rabindranath Tagore.
 

Asíntotas

Se llama asíntota de una función f(x) a una recta t cuya distancia a la curva tiende a cero, cuando x tiende a infinito o bien x tiende a un punto a.

Definición

Asíntota vertical

La recta x=a es asíntota vertical (AV) de f(x) si 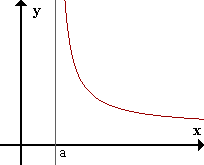limx->a+ f(x) = inf o limx->a- f(x) = inf.

Definición

Asíntota horizontal

La recta y=b es asíntota horizontal (AH) de f(x) si 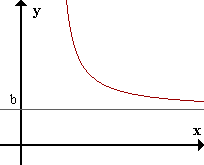limx->inf f(x) = b.

Ejemplo

f(x) = x/(x-1)

limx->1+ f(x) = +inf
limx->1- f(x) = -inf

=> x=1 es AV de f(x)

limx->inf f(x) = 1

=> y=1 es AH de f(x) 		      

Definición

Asíntota oblicua

La recta y = mx + n es asíntota oblicua (AO) de f(x) si 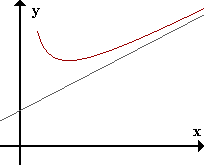limx->inf f(x) - (mx + n) = 0.

Ejemplo

f(x) = x + 1/x

limx->inf f(x) - x = limx->inf x + 1/x - x = 0

=> y=x es AO de f(x)

Además,
limx->0+ f(x) = +inf
limx->0- f(x) = -inf
=> x=0 es AV de f(x) 		   

Teorema

y = mx + n es asíntota oblicua de f(x) <=>
n = limx->inf f(x) - mx
m = limx->inf f(x)/x

Demostración:

Directo: 
Por hipótesis lim f(x) - (mx + n) = 0
              x->inf
				
=> lim f(x) - mx - n = 0 
   x->inf
   
=> lim f(x) - mx = n
   x->inf                                 
                                               n 
                                            ---^---
         f(x)          f(x)                f(x) - mx
=> lim   ---- = lim    ---- - m + m = lim  --------- + m = m
   x->inf x     x->inf  x             x->inf   x
Recíproco: 
lim f(x) - (mx + n) = lim f(x) - mx - n = 0
x->inf                x->inf
=> por definición y = mx + n es asíntota oblicua de f(x).

Página principal

Tabla de Contenidos

Noticias matemáticas
 
Cálculo > Asíntotas
Asíntotas

Última modificación: noviembre 2004
Página principal     Tabla de contenidos     E-mail