Derivada
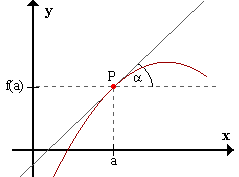
Consideremos la tangente a la curva f(x) en el punto P(a,f(a)).
¿Cómo se obtiene el ángulo α entre la tangente y el eje x positivo?
El conocimiento de los valores a y f(a) no basta para determinarlo, puesto que hay un número
infinito de rectas, aparte de la tangente, que pasan por P.
Tampoco es necesario conocer la función f(x) en su comportamiento global; el conocimiento
de la función en una vecindad arbitraria del punto P debe ser suficiente para determinar α.
Esto indica que se debería definir la dirección de la tangente a una curva f(x)
mediante un proceso de límite.
Consideremos un segundo punto P'(x,f(x)) sobre la curva, cercano a P.
Por los dos puntos P y P' se traza una línea recta.
Si el punto P' se mueve a lo largo de la curva hacia el punto P, entonces la recta PP' se aproxima
a la tangente.
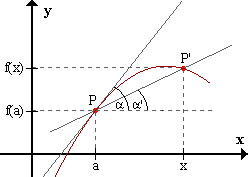
Sea α' el ángulo que la recta PP' forma con el eje x positivo.
Entonces limP'->P α' = α
Considerando las coordenadas de los puntos P y P', se tiene:
f(x) - f(a) cateto opuesto
tan α' = ----------- ( ---------------- )
x - a cateto adyacente
Así, nuestro proceso de límite está representado por la ecuación:
f(x) - f(a)
tan α = lim tan α' = lim -----------
x->a x->a x - a
A este límite se lo denomina derivada de la función f(x) en el punto a y se denota f'(a)
Definición
Derivada en el punto a
Se llama derivada de f(x) en x=a, y se denota f'(a) a:
f(x) - f(a)
f'(a) = lim -----------
x->a x - a
Función derivada
La derivada es una función de x, puesto que un valor de f'(x)
corresponde a cada valor de x.
Si una función es derivable, entonces es continua.
H) f es derivable en x=a.
T) f es continua en x=a.
Demostración:
Por hipótesis, existe
f(x) - f(a)
lim ----------
x->a x - a
=> existe f(a) (1)
lim f(x) = lim f(x) - f(a) + f(a) =
x->a x->a
f'(a) por H)
------^------ 0
(f(x) - f(a)) --^--
lim -------------(x - a) + f(a) = f(a) (2)
x->a x - a
De 1) y 2): existe f(a) y limx->af(x)=f(a) =>
por definición de continuidad, f es continua en x=a.
El recíproco no es cierto. Una función puede ser continua en un punto pero no derivable.
Cualquier curva con una esquina o vértice en un punto no posee ahí una tangente. Esos
puntos se llaman singulares, y esas funciones, funciones singulares.
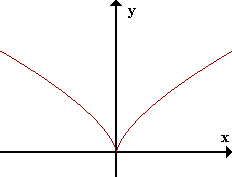
|
|
3 ___
f(x)= \|x2
no es derivable en x=0 pero es continua.
|
Derivada de las funciones elementales
-
f(x) = k
k - k
f'(a) = lim ------- = 0
x->a x - a
=> f'(x) = 0
-
f(x) = bx + c
bx + c - ba - c b(x - a)
f'(a) = lim --------------- = lim -------- = b
x->a x - a x->a x - a
=> f'(x) = b
-
f(x) = xn
xn - an
f'(a) = lim --------- =
x->a (x-a)
(x - a)(xn-1 + axn-2 + a2xn-3 + ... + an-1)
lim ------------------------------------------ = nan-1
x->a (x-a)
=> f'(x) = nxn-1
-
f(x) = bxn
bxn - ban b(xn - an)
f'(a) = lim ---------- = lim ----------- = bnan-1
x->a x - a x->a x - a
=> f'(x) = bnxn-1
-
f(x) = Lx equiv. a x/a - 1 (límites tipo)
--^--
Lx - La L(x/a) x - a 1
f'(a) = lim -------- = lim ------- = lim --------- = --
x->a x - a x->a x - a x->a a(x - a) a
1
=> f'(x) = ---
x
-
f(x)=logcx
logcd = Ld/Lc
|
logcx - logca logc(x/a) | logc(x/a) 1
f'(a)=lim ------------- = lim ---------- = lim --------- = ---
x->a x - a | x->a (x - a) x->a Lc(x - a) aLc
|
log a - log b = log(a/b)
1
=> f'(x) = ---
xLc
-
f(x) = ex
equiv. a 1 (límites tipo)
---^---
ex - ea ea(ex-a - 1)
f'(a) = lim --------- = lim ------------ = ea
x->a x - a x->a x - a
=> f'(x) = ex
-
f(x) = bx
equiv. a (x-a)Lb (límites tipo)
----^----
bx - ba ba(bx-a - 1) ba(x - a)Lb
f'(a)=lim ------- = lim ------------ = lim ----------- = baLb
x->a x - a x->a x - a x->a x - a
=> f'(x) = bxLb
-
f(x) = sen x
equiv. a (x-a)/2 (límites tipo)
-----^-----
senx - sena 2sen((x-a)/2)cos((x+a)/2)
f'(a)=lim ------------ = lim ------------------------- =
x->a x - a x->a x - a
2(x - a)cos((x+a)/2)
lim ------------------- = cos a
x->a 2(x - a)
=> f'(x) = cosx
-
f(x) = cosx
cos x - cos a -2sen((x-a)/2)sen((x+a)/2)
f'(a) = lim ------------- = lim -------------------------- =
x->a x - a x->a x - a
-2(x-a)sen((x+a)/2)
lim ------------------- = -sen a
x->a 2(x - a)
=> f'(x) = -senx
-
f(x) = tgx
1 (límites tipo)
---^---
tgx - tga (*) tg(x-a)
f'(a)=lim ---------- = lim ------- (1 + tgx.tga) = 1 + tg2a
x->a x - a x->a (x-a)
tgx - tga
(*) Pues tg(x - a) = ------------
1 + tgx.tga
sen2a cos2a + sen2a 1
1 + ------ = ------------- = ----
cos2a cos2a cos2a
1
=> f'(x)=1 + tg2x = -------
cos2x
n __
f(x)= \|x
n __
\|x = x1/n
1 x(1-n)/n 1 1
f'(x)=(x1/n)'= --x1/n - 1 = ----------- = ------- = --------
n n nx(n-1)/n n ____
n \|xn-1
1
=> f'(x) = ---------
n ____
n \|xn-1
siguiente >>
|



