• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Límite finito

Definición

Intervalo cerrado

Un segmento en el eje numérico con extremos a y b, con a < b, se denomina intervalo. Si los puntos extremos, a y b, están incluidos en el intervalo, se dice que el intervalo es cerrado, y se denota por [a,b].
[a,b] = { x perteneciente a R / a <= x <= b }

El intervalo cerrado [a,b] consiste de los puntos x para los cuales a <= x <= b.

Definición

Intervalo abierto

Si los puntos extremos se excluyen, el intervalo se llama abierto, y se denota por (a,b).
(a,b) = { x perteneciente a R / a < x < b }

El intervalo abierto (a,b) consiste de aquellos puntos x para los cuales a < x < b.

Definición

Entorno del punto a de radio δ

Es el intervalo abierto (a - δ,a + δ), esto es, consiste de los valores x para los cuales a - δ < x < a + δ.
E_a,δ = { x perteneciente a R / |x - a| < δ }

Son los puntos x cuya distancia al punto a es menor que δ.

Definición

Entorno reducido de a de radio δ

No incluye al punto a.
E^*_a,δ = { x perteneciente a R / 0 < |x - a| < δ }

Son los puntos x cuya distancia al punto a es menor que δ pero mayor que 0, es decir, no se incluye a a.

El concepto de Límite

Consideremos la función f(x)=x².

Observemos los valores de f(x) para x cercanos a 3.

Cuando x se aproxima a 3, los valores de f(x) se acercan a 9. Se dice que f(x) tiende a 9 cuando x tiende a 3.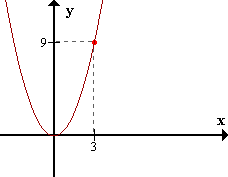

En general, una función f(x) tiende a un límite b cuando x tiende a a, si f(x) difiere arbitrariamente poco de b para todo x situado suficientemente cerca de a.
En símbolos, lim_x->af(x)=b.

Enseguida se expresa más precisamente la definición de límite.

Definición

Límite finito de una función

lim_x->a f(x)=b <=> para todo ε>0 existe δ>0 / para todo x, 0 < |x-a| < δ |f(x) - b| < ε.

Otra notación:
lim_x->a f(x)=b <=> para todo E_b,ε existe un E^*_a,δ / para todo x perteneciente al E^*_a,δ f(x) pertenece a E_b,ε.

Se dice que la función f(x) tiene límite b, cuando x tiende a a, si dado ε positivo arbitrario y tan pequeño como se quiera, existe un δ tal que para todo x perteneciente al entorno reducido de a de radio δ, la función pertenece al entorno de b de radio ε.

Dicho de otro modo, para cualquier número positivo ε, por pequeño que sea, podemos encontrar un δ tal que para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) está dentro del entorno de b de radio ε.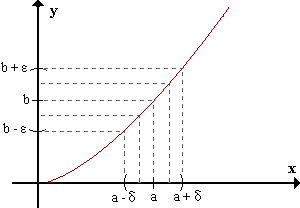

lim_x->af(x)=b significa que por más pequeño que sea el entorno considerado alrededor de b, va a ser posible encontrar un entorno de a, para cuyos valores x (x ≠ a), la función f da como resultado valores que están dentro del entorno de b considerado.

En otras palabras, la función f(x) tiene límite b, cuando x tiende a a, si el valor de la función f(x) se hace arbitrariamente próximo al valor b cuando x se aproxima al valor a.

Notar que la definición dice entorno reducido de a. Es decir que f(a) puede no existir, o puede estar fuera del entorno de b, pero el límite de f cuando x tiende a a sigue siendo b.

f(a) ≠ b, pero limx->af(x)=b

siguiente >>

Cálculo > Límite finito

Límite finito – Teoremas – Límite infinito – Operaciones con límites – Límites de polinomios – Límites tipo – Infinitésimos – Infinitos – Cálculo de límites – Ejercicios