
Acostarse temprano y levantarse temprano, hace a un hombre sano, rico y sabio.
Benjamin Franklin.
 |
Acostarse temprano y levantarse temprano, hace a un hombre sano, rico y sabio. Benjamin Franklin. |
Continuidad
Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva.
En contraste, una gráfica como la de la función f(x) = sgn x (signo de x) que consiste de pedazos de curva separados por un vacío en una abcisa exhibe allí una discontinuidad.
La continuidad de la función f(x) para un valor a significa que f(x) difiere arbitrariamente
poco del valor f(a) cuando x está suficientemente cerca de a. Expresemos esto en términos del concepto de límite... DefiniciónContinuidad
Una función f(x) es continua en un punto a si
Nota: observar que debe existir f(a) y debe existir el Ejemplos de discontinuidad
Sin embargo, si miramos la función para x próximos a 2 pero menores, e ignoramos los x mayores que 2, la función es continua en 2 "por la izquierda". DefiniciónContinuidad por la izquierda
Una función f(x) es continua por la izquierda en el punto a si existe f(a) y DefiniciónContinuidad por la derecha
Una función f(x) es continua por la derecha en el punto a si existe f(a) y La función anterior es continua por la izquierda en x=2, pero no por la derecha. DefiniciónContinuidad en un intervalo cerrado [a,b]
Una función f(x) es continua en un intervalo cerrado [a,b] si: Clasificación de discontinuidadesEvitableCaso A:No existe f(a) pero existe limx->af(x). Ejemplo:
No existe f(0) pues anula un denominador. limx->0-f(x) = limx->0+f(x) = 2 o sea limx->0f(x)=2 Podemos extender la definición de la función, asignándole en el punto a el valor del límite, con lo cual la función se torna continua. Por ello este tipo de discontinuidad se denomina evitable. Caso B:
Existe f(a) y existe limx->af(x)=b pero b≠f(a). Ejemplo:
f(2) = 8 Asignándole a la función el valor 4 en x=2, se elimina la discontinuidad. No evitable1ª especie:
limx->a-f(x) ≠ limx->a+f(x). Ejemplo:
limx->2-f(x) = -inf 2ª especie:
No existe limx->a-f(x) o no existe limx->a+f(x). Ejemplo:
En x=-2 y x=2 la función presenta discontinuidades no evitables de 2ª especie. No existe limx->-2+f(x) y no existe limx->2-f(x). Operaciones con funciones continuasSi f y g son funciones continuas en x=a, la suma, multiplicación y cociente de f y g (con g(a) ≠ 0) son funciones continuas en x=a.
H) f(x) es continua en x=a. Por definición de continuidad,
existe f(a) y existe limx->af(x) = f(a) => por teo. límite de la suma de funciones, el límite de una suma de funciones es igual a la suma de los límites de cada función, si éstos son finitos. limx->a f(x) + g(x) = f(a) + g(a) => por def. de continuidad f(x) + g(x) es continua en x=a. Análogamente se prueba la continuidad del producto y el cociente. TeoremaContinuidad de la función compuesta
H) f es continua en x=a. Demostración: Queremos demostrar que limx->a g[f(x)]=g[f(a)], o sea, por definición de límite, queremos probar que, dado ε>0 existe δ>0 tal que para todo x perteneciente al E*a,δ g[f(x)] perteneciente al Eg[f(a)],ε.
Por hipótesis g es continua en f(a) => por def. de continuidad
para todo x perteneciente al E*f(a),δ g(x) pertenece al Eg[f(a)],ε (1) Por hipótesis f es continua en a => por def. de continuidad limx->af(x) = f(a), es decir que (por def. de límite) si tomamos el número δ de (1), existe α>0 tal que... para todo x perteneciente al E*a,α f(x) pertenece al Ef(a),δ (2)
De (1) y (2) se deduce que: 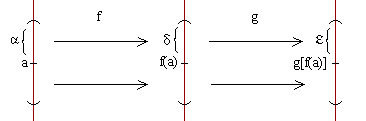
siguiente >> |
Página principal Tabla de Contenidos Noticias matemáticas |
||||||||||||||||||||||||||
|
|
|
Última modificación: noviembre 2007 Página principal Tabla de contenidos E-mail |