• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Sucesiones

Definición

Sucesión

Se denomina sucesión a una función cuyo dominio es el conjunto de los números naturales.

Para denotar el n-ésimo elemento de la sucesión se escribe a_n en lugar de f(n).

Ejemplo:

a_n = 1/n

a₁ = 1, a₂ = 1/2, a₃ = 1/3, a₄ = 1/4, ...

Definición

Sucesión monótona creciente

Una sucesión es monótona creciente si se cumple que para todo n natural a_n <= a_n+1 (a₁ <= a₂ <= a₃ <= ... <= a_n).

Ejemplo:

a_n = n es monótona creciente.

a₁ = 1, a₂ = 2, a₃ = 3, a₄ = 4, ...

Definición

Sucesión monótona decreciente

Una sucesión es monótona decreciente si se cumple que para todo n natural a_n >= a_n+1 (a₁ >= a₂ >= a₃ >= ... >= a_n).

Ejemplo:

a_n = 1/n es monótona decreciente.

a₁ = 1, a₂ = 1/2, a₃ = 1/3, a₄ = 1/4, ...

Límite finito de una sucesión

Consideremos la sucesión a_n = 1/n.

a₁ = 1
a₂ = 1/2 = 0.5
a₃ = 1/3 ≈ 0.33
a₄ = 1/4 = 0.25
a₅ = 1/5 = 0.2
a₆ = 1/6 ≈ 0.17
a₇ = 1/7 ≈ 0.14
a₈ = 1/8 ≈ 0.12
a₉ = 1/9 ≈ 0.11
a₁₀ = 1/10 = 0.1

A medida que aumenta n, los términos de la sucesión son cada vez más cercanos a 0. Si representamos los términos como puntos en una línea, esto significa que los puntos a_n se apiñan cada vez más cerca del punto 0 conforme n crece.

Se dice que a_n tiende a 0, o que tiene límite 0.
Se expresa simbólicamente por: lim a_n = 0 o bien, ocasionalmente, por la notación abreviada a_n -> 0.

Límite finito

lim a_n = a <=> para todo ε>0 existe N natural / para todo n > N a - ε < a_n < a + ε, o lo que es lo mismo, |a_n - a| < ε.

Para cualquier número positivo ε, por pequeño que sea, podemos encontrar un natural N suficientemente grande tal que a partir del índice N en adelante se tiene que |a_n - a| < ε.
Es decir, si tomamos un entorno de a de cualquier radio siempre habrá un subíndice N tal que desde N en adelante todos los términos de la sucesión pertenecen a dicho entorno.

Límite infinito de una sucesión

Consideremos la sucesión a_n = n².

a₁ = 1
a₂ = 4
a₃ = 9
a₄ = 16
...
a₁₀ = 100
...
a₁₀₀ = 10.000

Al crecer n, a_n no tiende a un límite definido, sino que crece más allá de toda cota. Se dice que a_n tiende a infinito.

Definición

Límite infinito

lim a_n = +inf <=> para todo K>0 existe N natural / para todo n > N a_n > K.

Para cualquier número positivo K (tan grande como se quiera), podemos encontrar un natural N, tal que a_N y todos los términos siguientes son mayores que K. Esto quiere decir que a_n puede hacerse mayor que cualquier cota, con tal de que n sea lo suficientemente grande.

Del mismo modo se define lim a_n = -inf <=> para todo K<0 existe N natural / para todo n > N a_n < K.

Definición

Convergencia y divergencia

Cuando una sucesión tiene límite finito a se dice que es convergente y converge a a.
Una sucesión que tiene límite infinito se llama divergente.
Una sucesión que carece de límite se llama oscilante.

La sucesión a_n = 1/n converge a 0.
La sucesión a_n = n² es divergente.
La sucesión a_n = sen n es oscilante, pues sus valores varían entre 1 y -1.

Propiedades del límite finito de sucesiones

Unicidad del límite

Si una sucesión tiene límite es único.

H) lim a_n = b
T) b es único

La demostración se hace por reducción al absurdo.
Suponemos que a_n tiene dos límites distintos b y c.
Suponemos que b > c.

lim a_n = b => (por def. de límite finito de una sucesión) para todo ε>0 existe n₁ natural / para todo n > n₁ b - ε < a_n < b + ε;

lim a_n = c => (por def. de límite finito de una sucesión) para todo ε>0 existe n₂ natural / para todo n > n₂ c - ε < a_n < c + ε

Consideremos un ε tal que 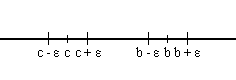c+ε < b-ε, o sea ε < (b - c)/2

Sea N = max {n₁,n₂}

Para todo n > N se cumple

• b - ε < a_n < b + ε
• c - ε < a_n < c + ε

Absurdo, pues a_n no puede pertenecer a dos entornos disjuntos.
Absurdo de suponer b ≠ c.
Por lo tanto b = c.

Límite de la sucesión comprendida

Si una sucesión está comprendida entre otras dos que tienen igual límite, entonces tiene el mismo límite.

H) lim a_n = lim b_n = p
    Para todo n > n₀ a_n <= c_n <= b_n
T) lim c_n = p

lim a_n = p => (por def. de límite de una sucesión) para todo ε₁ > 0 existe n₁ natural / para todo n > n₁ p - ε₁ < a_n < p + ε₁

lim b_n = p => (por def. de límite de una sucesión) para todo ε₂ > 0 existe n₂ natural / para todo n > n₂ p - ε₂ < b_n < p + ε₂

Sea N = max {n₀, n₁, n₂}

Para todo n > N se cumple p-ε₁ < a_n <= c_n <= b_n < p+ε₂

p-ε₁ < c_n < p+ε₂

Sea ε = min {ε₁, ε₂}

Para todo n > N p-ε < c_n < p+ε

=> (por def. de límite de una sucesión) lim c_n = p.

Operaciones con límites

El límite de la suma, producto y cociente de sucesiones se determina por las mismas reglas que para las funciones de variable continua. Las demostraciones son iguales, basta sustituir f(x) por a_n y considerar que la tendencia siempre es hacia +infinito. Aquí sólo demostraremos el límite de una suma. Para ver las demás reglas visitar la página sobre operaciones con límites.

Si dos sucesiones tienen límite finito, entonces su suma tiene límite finito y es igual a la suma de esos límites.

H) lim a_n = a, lim b_n = b
T) lim a_n + b_n = a + b

Queremos probar que, dado ε > 0, existe N > 0 tal que para todo n > N |(a_n + b_n) - (a+b)| < ε.

Sea ε' = ε/2

lim a_n = a => (por def. de límite finito de una sucesión) para todo ε' > 0 existe n₀ natural / para todo n > n₀ |a_n - a| < ε'.

lim b_n = b => (por def. de límite finito de una sucesión) para todo ε' > 0 existe n₁ natural / para todo n > n₁ |b_n - b| < ε'.

Sea N = max {n₀, n₁}

Para todo n > N se cumple:

• |a_n - a| < ε'
• |b_n - b| < ε'

=> |a_n - a| + |b_n - b| < 2ε' = ε

|(a_n + b_n) - (a+b)| = |(a_n - a) + (b_n - b)| <= (*) |a_n - a| + |b_n - b| < ε

(*) Desigualdad triangular: |x + y| <= |x| + |y|

Resumiendo, dado ε>0 existe N / para todo n > N |(a_n + b_n) - (a+b)| < ε

=> (por def. de límite finito de una sucesión) lim a_n + b_n = a + b

Definición

Sucesiones equivalentes

Dos sucesiones se dicen equivalentes cuando el límite de su cociente es 1.

Sucesión acotada

M es cota superior de la sucesión a_n si a_n < M para todo n.
m es cota inferior de la sucesión a_n si a_n > m para todo n.
Una sucesión es acotada si tiene tanto cota superior como inferior.

Toda sucesión monótona y acotada converge.

H) a_n monótona
    Existen m y M / m < a_n < M para todo n.
T) lim a_n = b

Queremos probar que existe N / para todo n > N |a_n - b| < ε.

Supongamos que a_n es creciente (si suponemos que es decreciente, la demostración es análoga).

a_n < M para todo n

Es decir que el conjunto de todos los términos de la sucesión S = {a₁, a₂, a₃, ...} tiene extremo superior (la menor de las cotas superiores), llamémosle b.

Sea ε>0

b - ε no es cota superior de S pues es menor que el extremo superior

=> existe N / a_N > b-ε.

a_n es creciente => para todo n > N a_n >= a_N => a_n > b-ε => -(a_n - b) < ε (1)

b+ε también es cota superior de S

=> para todo n a_n < (b+ε) => => a_n - b < ε (2)

=> De 1) y 2) para todo n > N |a_n - b| < ε

Teorema

Toda sucesión convergente es acotada.

H) a_n convergente
T) a_n acotada

a_n es convergente, eso significa que tiene límite finito: lim a_n = a

=> (por def. de límite finito de una sucesión) para todo ε>0 existe N / para todo n > N a-ε < a_n < a+ε

=> (por def. de sucesión acotada) a_n está acotada.

Nota: El recíproco no es cierto. Que una sucesión esté acotada no implica que sea convergente.

Contraejemplo: a_n = (-1)ⁿ está acotada pero no es convergente.

-1, 1, -1, 1, -1, 1, -1, 1, ...

Par de sucesiones monótonas convergentes

((a_n),(b_n)) es un par de sucesiones monótonas convergentes si
a) a_n es creciente y b_n decreciente.
b) Para todo n natural a_n <= b_n
c) Para todo ε>0 existe h natural / b_h - a_h < ε

Ejemplo:

a_n = -1/n, b_n = 1/n

-1    -1    -n + n + 1     1
--- - --- = ---------- = ------ > 0
n+1    n      n(n+1)     n2 + n

 1     1    n + 1 - n     1
--- - --- = --------- = ------ > 0
 n    n+1     n(n+1)    n2 + n

-1     1
--- < --- pues -n < n para todo n.
 n     n

Dado ε>0, existe h / b_h - a_h < ε

 1    -1     2                          
--- - --- = --- < ε 
 h     h     h                          

Para que se cumpla basta tomar un h > 2/ε

Propiedad

Todo PSMC tiene frontera

((a_n),(b_n)) es un PSMC => existe c / para todo n a_n <= c <= b_n, lim a_n = c- y lim b_n = c+.

lim a_n = c- significa que a_n se aproxima a c por la izquierda, y lim b_n = c+ significa que b_n se aproxima a c por la derecha.

El número e

A menudo un número a se describe por medio de una sucesión infinita a_n de aproximaciones; esto es, el valor a está dado por el valor a_n con cualquier grado de precisión deseado si el índice n se elige suficientemente grande.

Este es el caso del número e (e = 2,718281...), que puede definirse como el límite de la sucesión a_n = (1 + 1/n)ⁿ o de la sucesión b_n = (1 + 1/n)ⁿ⁺¹.

Probaremos que estas sucesiones forman un PSMC.

                                                          
                   n  n               n     n!        
an = (1 + 1/n)n  = Σ Ci.1n-i.(1/n)i = Σ   ---------- 
                  i=0                i=0 (n-i)!i!ni   

                                                            
                       n+1 n+1                  n+1    (n+1)!
an+1=(1 + 1/(n+1))n+1 = Σ  Ci.1n+1-i.(1/(n+1))i = Σ  ----------------
                       i=0                      i=0 (n+1-i)!i!(n+1)i

   n!       ?      (n+1)!
---------- <= ---------------
(n-i)!i!ni    (n+1-i)!i!(n+1)i

n(n-1)...(n-i+1)  ? (n+1)(n)...(n+1-i+1)  --> i factores
---------------- <= --------------------
    n.n....n         (n+1)(n+1)...(n+1)   --> i factores
	
(n-1)   (n-i+1)  ?  n    n+1-i+1
-----...------- <= ---...-------
  n	   n       n+1     n+1
  
      1          i-1   ?       1          i-1
(1 - ---)...(1 - ---) <= (1 - ---)...(1 - ---)
      n           n           n+1         n+1

bn = (1 + 1/n)n+1
bn+1 = (1 + 1/n+1)n+2 = (1 + 1/n+1)n+1.(1 + 1/n+1)
     ?
bn+1 <= bn
                           ?
(1 + 1/n+1)n+1.(1 + 1/n+1) <= (1 + 1/n)n+1

 (1 + 1/n)n+1   ?      1
-------------- >= 1 + ---
(1 + 1/n+1)n+1        n+1

   n+1/n   n+1   ?      1
( ------- )     >= 1 + ---
  n+2/n+1              n+1

  n2 + 2n + 1  n+1  ?      1
( ----------- )    >= 1 + ---
    n2 + 2n               n+1    
  
         1    n+1  ?      1
( 1 + ------- )   >= 1 + ---		
      n2 + 2n            n+1

         1    n+1          n+1
( 1 + ------- )   >= 1 + -------		
      n2 + 2n            n2 + 2n
	  
      n+1  ?       1  
1 + ------ >= 1 + ---
    n2 + 2n       n+1
	
  n+1   ?   1
------- >= ---
n2 + 2n    n+1

n2 + 2n + 1 > n2 + 2n se cumple para todo n.

an = (1 + 1/n)n
bn = (1 + 1/n)n+1

        ?
bn - an > 0
                      ?
(1+1/n)n+1 - (1+1/n)n > 0

(1+1/n)n(1+1/n - 1) = 1/n(1+1/n)n > 0 para todo n >= 1.

                               (1)      (2)
bn - an = 1/n(1+1/n)n = (1/n)an < (1/n)bn < (1/n)b1 = (1/n)4 < ε

n=1:      2 < e < 4
n=2:   2,25 < e < 3,375
n=3:   2,37 < e < 3,16
n=4:   2,44 < e < 3,05
...
n=100: 2,70 < e < 2,73

Sucesiones y series

Sucesiones – Series – Ejercicios