No hay más que un modo de dar en el clavo, y es dar ciento en la herradura.
Miguel de Unamuno.
 

Ejercicios

Recordar que con frecuencia existen varias vías para resolver un problema dado.
Tener en cuenta también que resulta muy útil hacer esquemas o dibujos para visualizar mejor los problemas.

Reglas de la suma y el producto

  1. ¿Cuántas palabras de tres letras se pueden formar con cinco consonantes y tres vocales de modo que cada palabra comience y termine en consonante? 
     C   V   C
--- --- ---       5.3.4 = 60   (regla del producto)
 5   3   4
  2. Determine el número de enteros de seis dígitos (que no comiencen con cero) en los que
    1. ningún dígito se pueda repetir. 
       9   9   8   7   6   5
--- --- --- --- --- ---

9.9.8.7.6.5 = 136.080   (regla del producto)
    2. se pueden repetir los dígitos. 
      9.10.10.10.10.10 = 900.000   (regla del producto)

  3. Ana y María vieron a dos hombres alejarse en automóvil frente a una joyería, justo antes de que sonara una alarma contra robos. Cuando fueron interrogadas por la policía, las dos jóvenes dieron la siguiente información acerca de la placa (que constaba de dos letras seguidas de cuatro dígitos). María estaba segura de que la segunda letra de la placa era una O o una Q, y que el último dígito era un 3 o un 8. Ana dijo que la primera letra de la placa era una C o una G y que el primer dígito era definitivamente un 7.
    ¿Cuántas placas diferentes tendrá que verificar la policía? 

     C/G    Q/O     7    0 a 9  0 a 9  8 ó 3
-----  -----  -----  -----  -----  ----- 
  |     |       |      |      |      |
  2  x  2   x   1  x  10  x  10   x  2 = 800   (regla del producto)

  4. Tres pueblos, designados como A, B y C, están intercomunicados por un sistema de carreteras de doble sentido.

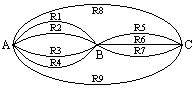
    1. ¿De cuántas formas puede Juan ir del pueblo A al pueblo C?

      2 + 4.3 = 14 (reglas de la suma y del producto)

    2. ¿Cuántos trayectos puede hacer Juan del pueblo A al pueblo C y de regreso al pueblo A?

      14.14 = 196 (regla del producto)

    3. ¿Cuántos de los trayectos completos de la parte (b) son tales que el viaje de regreso (del pueblo C al pueblo A) es diferente, al menos parcialmente, de la ruta que toma Juan del pueblo A al pueblo C? (Por ejemplo, si Juan viaja de A a C por las rutas R1 y R6 podría regresar por las rutas R6 y R2, pero no por R1 y R6).

      14.13 = 182 (regla del producto)

Permutaciones


    1. ¿Cuántas permutaciones existen para las ocho letras a,b,c,d,e,f,g,h?

      P8 = 8! = 40.320.

    2. ¿Cuántas de las permutaciones de (a) comienzan con la letra a?

      P7 = 7! = 5.040.

    3. ¿Cuántas de las permutaciones de (a) comienzan con la letra a y terminan con la letra c?

      P6 = 6! = 720.

  2. ¿De cuántas formas es posible ordenar los símbolos a,b,c,d,e,e,e,e,e de modo que ninguna e quede junto a otra? 
    e _ e _ e _ e _ e

P4 = 4! = 24
    1. ¿De cuántas maneras se pueden colocar las letras de VISITING?

      Si consideramos que las tres I son distintas, podemos formar P8 palabras. Así, la permutación VI1SI2TI3NG sería distinta de VI2SI1TI3NG. Pero esto no es lo que queremos, en realidad no hay diferencia entre esas dos permutaciones. Como las tres I pueden ubicarse de P3 maneras, cada palabra se está repitiendo P3 veces. Por lo tanto hay P8/P3 = 8!/3! = 6.720 disposiciones diferentes.

    2. ¿Cuántas de ellas tienen las tres letras I juntas?

      Las restantes 5 letras pueden ordenarse de P5 formas. Las 3 letras I pueden ubicarse en 6 posiciones diferentes: al principio, al final o en cualquiera de los 4 espacios entre las otras 5 letras. Así, hay 6.5! = 6! = 720 palabras con las tres I juntas. 
      III_ _ _ _ _
_III_ _ _ _
_ _III_ _ _
_ _ _III_ _
_ _ _ _III_
_ _ _ _ _III

Combinaciones

  1. Un estudiante que realiza un examen debe responder 7 de las 10 preguntas. El orden no importa. ¿De cuántas formas puede responder el examen?

    Existen 
     10  10!   10.9.8
C7 = --- = ------ = 120
     7!3!   3.2.1
    combinaciones posibles de preguntas que puede contestar.

  2. Juan quiere dar una fiesta para algunos de sus amigos. Debido al tamaño de su casa, sólo puede invitar a 11 de sus 20 amigos. ¿De cuántas formas puede seleccionar a los invitados?

    Hay 
     20    20!
C11 = ---- = 167.960
      11!9!
    formas de elegir a los 11 amigos.

  3. En una reunión de 6 personas, ¿cuántos saludos de mano pueden intercambiarse, si entre cada 2 personas, se dan la mano una sola vez? 

     6    6!    6.5
C2 = ---- = --- = 15
     2!4!    2

  4. Una persona que sale de vacaciones desea llevarse 4 libros para leer: dispone de 4 novelas policiales y 6 libros de cuentos cortos. ¿De cuántas formas puede hacer la elección si quiere llevar al menos una novela? 

                          6
 N   C   C   C  --> 4C3 = 80
                     4 6
 N   N   C   C  --> C2C2 = 90     
                     4
 N   N   N   C  --> C36 = 24
                   
 N   N   N   N  --> 1
                         
80 + 90 + 24 + 1 = 195

  5. ¿Cuántos bytes contienen

    1. exactamente dos unos? 
       8    8!
C2 = --- = 28  
     2!6!
		  
Ejemplo:  1   0   0   1   0   0   0   0
    2. exactamente cuatro unos? 
       8    8!
C4 = --- = 70
     4!4!
		  
Ejemplo:  0   1   0   1   0   1   1   0
    3. exactamente seis unos? 
       8    8!
C2 = --- = 28
     6!2!
		  
Ejemplo:  1   1   1   0   1   1   0   1
    4. al menos seis unos? 
            8
28 + C7 + 1 = 28 + 8 + 1 = 37 
(Sumamos los bytes con 6 unos, los
 bytes con 7 unos y el byte con 8 unos)
	
Ejemplo:  1   1   1   0   1   1   1   1
  6. ¿De cuántas formas es posible distribuir 12 libros diferentes entre cuatro niños de modo que
    1. cada niño reciba tres libros. 
       12 9  6  3
C3.C3.C3.C3 = 220.84.20.1 = 369.600
    2. los dos niños mayores reciban cuatro libros cada uno y los dos menores reciban dos libros cada uno. 
       12 8  4      12!8!4!
C4.C4.C2 = ------------ = 207.900
            8!4!4!4!2!2!

  7. Un comité de 12 personas será elegido entre 10 hombres y 10 mujeres. ¿De cuántas formas se puede hacer la selección si

    1. no hay restricciones? 
       20    20 !   
C12 = ----- = 125.970
      12!8!
    2. debe haber seis hombres y seis mujeres? 
       10 10  10!10! 
C6.C6 = -------- = 44.100
        6!4!6!4!
    3. debe haber un número par de mujeres? 
                                                  10 10
Si hay 2 mujeres, debe haber 10 hombres => C2.C10

                              10            10 10
Si hay 4 mujeres, debe haber C8 hombres => C4.C8

                              10            10 10
Si hay 6 mujeres, debe haber C6 hombres => C6.C6

                              10            10 10
Si hay 8 mujeres, debe haber C4 hombres => C8.C4

                               10            10  10
Si hay 10 mujeres, debe haber C2 hombres => C10.C2

 5  10  10
 Σ C2i.C12-2i = 63.090
i=1
    4. debe haber más mujeres que hombres? 
                                10 10
7 mujeres y 5 hombres => C7.C5
                          10 10
8 mujeres y 4 hombres => C8.C4
                          10 10
9 mujeres y 3 hombres => C9.C3
                           10 10
10 mujeres y 2 hombres => C10.C2

    10  10 10
=>  Σ  Ci.C12-i
   i=7
    5. debe haber al menos 8 hombres? 
                                10 10
8 hombres y 4 mujeres => C8.C4
                          10 10
9 hombres y 3 mujeres => C9.C3
                           10  10
10 hombres y 2 mujeres => C10.C2

    10  10 10
=>  Σ  Ci.C12-i
   i=8
  8. Resolver el siguiente sistema. 
     20   20
Ca + Ca-1 = 21
 n      n-1  n-2   12
Ca+1 - Ca - Ca  = ------
                  Pa + 1

     20   20
Ca + Ca-1 = 21
--------- --> Stieffel
    21                        m
   Ca     = 21 => a = 1 pues C1 = m


  n    n-1  n-2    12
 C2 - C1 - C1   = --- = 6
---------           2     -->  Stieffel
    n-1     n-2         
   C2    - C1  = 6
   -----------            -->  Stieffel
        n-2
       C2      = 6

      (n-2)(n-3) = 12
      n2 - 5n + 6 = 12
      n2 - 5n - 6 = 0
                 _______                 6
           5 + \|25 + 24      5 + 7    /
       n = --------------- = ------- =        
                 2              2      \ 
                                        -1
       n = 6
  9. Resolver el siguiente sistema: 
      x    x+1
4Cy = Cy+1
 3x      3x        
C3y+1 = C12y-1

      x    x+1
4Cy = Cy+1
 
  4x!          (x+1)!
------- = ---------------
y!(x-y)!  (y+1)!(x+1-y-1)!

4x!(y+1)!(x-y)! = (x+1)!y!(x-y)!

4(y+1) = (x+1)

x = 4y + 4 - 1

x = 4y + 3 (1) 
 
 3x      3x
C3y+1 = C12y-1

=> Hay dos posibilidades:

      

    • 3y + 1 = 12y - 1 => 9y = 2 => y = 9/2 
No, pues y debe ser entero
      

    • 3y + 1 + 12y - 1 = 3x => 15y = 3x => 5y = x (2)
      
De 1) y 2) 5y = 4y + 3
           y = 3
           x = 15

Arreglos

  1. Cuatro nadadores van a disputar la final del campeonato mundial. Los premios son: 1º-medalla de oro, 2º-medalla de plata y 3º-medalla de bronce. ¿De cuántas maneras pueden ser distribuidas esas medallas? 

     4
A3 = 4! = 24
  2. Con los dígitos 0,1,2,3,4,5

    1. ¿Cuántos números de tres cifras se pueden formar?

      Se pueden formar A63 números. Pero están incluidos ahí los que comienzan con cero, que son A52. 
       6    5 
A3 - A2 = 100
      Por ejemplo 045 no es un número de tres cifras, sino de dos.

    2. ¿Cuántos son pares?

      Los que terminan en 0: 
       5
A2 = 20
      Los que terminan en 2 pero no comienzan con 0: 
       5    4
A2 - A1 = 16
      Los que terminan en 4 pero no comienzan con 0: 
       5     4
A2 - A1 = 16
      Total: 52
    1. ¿Cuántas palabras pueden formarse con las letras de la palabra TRIANGULO?

      P9 = 9! = 362.880

    2. ¿Cuántas comienzan con T y terminan en O?

       T                               O
--- --- --- --- --- --- --- --- ---
      P7 = 7! = 5.040
    3. ¿Cuántas tienen las 4 vocales juntas? 
      6.P5.P4 = 17.280
   |  |
   |  vocales 
   consonantes

V C1 C2 C3 C4 C5 
C1 V C2 C3 C4 C5 
C1 C2 V C3 C4 C5 
C1 C2 C3 V C4 C5 
C1 C2 C3 C4 V C5  
C1 C2 C3 C4 C5 V

    4. ¿En cuántas la A ocupa lugar impar?

       A       A       A       A       A
--- --- --- --- --- --- --- --- ---

5.P8 = 5.8! = 201.600
      Si la A está en el primer lugar, las restantes letras pueden disponerse de P8 maneras. Lo mismo si la A está en 3º, 5º, 7º o 9º lugar. Por lo tanto hay 5.P8 ordenaciones posibles.

    5. ¿En cuántas la A y la O ocupan lugares impares simultáneamente?

               A       O  
--- --- --- --- --- --- --- --- ---

      La A y la O se ubican en dos de 5 posiciones posibles: 1ª, 3ª, 5ª, 7ª y 9ª. Es decir, pueden ubicarse de 

       5
A2 formas.
      Las restantes 7 letras pueden disponerse de P7 formas. Por lo tanto, existen 
          5   7!5!
P7.A2 = ---- = 100.800
         3!
      ordenaciones posibles.
  4. Determinar el valor de n en cada uno de los siguientes casos: 
    1.  n
A2 = 90

        n!
------ = 90 => n(n-1) = 90 => n2 - n - 90 = 0
(n-2)!
          _______               10
    1 + \|1 + 490   1 + 19    / 
n = ------------- = ------ =  
         2a            2      \
                                -9
n=10

    2.  n     n          
A3 = 3A2

        n       3n!
----- = ------
(n-3)!  (n-2)!

n(n-1)(n-2) = 3n(n-1)
n-2 = 3
n = 5

    3.   n         24
2A2 + 50 = A2

       2n!           2n!
----- + 50 = -------
(n-2)!       (2n-2)!

2n(n-1) + 50 = 2n(2n-1)
2n2 - 2n + 50 = 4n2 - 2n
-2n2 + 50 = 0
n2 = 25
n = 5

<< anterior

Página principal

Tabla de Contenidos

Noticias matemáticas
 
Matemática discreta > Conteo
Definiciones – Ejercicios

Última modificación: noviembre 2004
Página principal     Tabla de contenidos     E-mail