• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Weierstrass

Antes que nada, veamos una definición y una propiedad relativas a sucesiones, que se emplearán en la demostración del lema de Weierstrass.

Definición: Par de sucesiones monótonas convergentes (PSMC)

((a_n),(b_n)) es un PSMC <=>
1) (a_n) es creciente
    (b_n) es decreciente
2) Para todo n natural a_n < b_n
3) Para todo ε > 0 existe n₀ natural / b_n0 - a_n0 < ε

Propiedad: Todo PSMC tiene frontera

((a_n),(b_n)) es un PSMC => existe c / para todo n a_n <= c <= b_n, lim a_n = c- y lim b_n = c+.

Lema de Weierstrass

Karl Weierstrass (1815-1897)

Una función continua en un intervalo cerrado está acotada.

H) f continua en [a,b]
T) f está acotada en [a,b]

Demostración:

La demostración se realiza por el absurdo. Esto es, se supone falsa la tesis y se llega a una contradicción.

Suponemos entonces que f(x) no está acotada en [a,b].

Dividamos el intervalo [a,b] a la mitad. Si f está acotada en una de las mitades, entonces no lo está en la otra. Tomemos esta mitad. Llamemos a₁ y b₁ a los extremos de este nuevo intervalo. f no está acotada en [a₁,b₁].
Dividamos [a₁,b₁] en dos intervalos iguales. Si f está acotada en uno de ellos, tomemos el otro, si no, tomemos cualquiera. Llamemos a sus extremos a₂ y b₂.
Continuando de esta manera, tenemos una sucesión de intervalos [a,b], [a₁,b₁], [a₂,b₂], etc., tales que a <= a₁ <= a₂ <= ... <= a_n y b >= b₁ >= b₂ >= ... >= b_n.

Es decir,
1) Los a_i forman una sucesión creciente y los b_i forman una sucesión decreciente.
2) Los a_i son siempre menores que los b_i.

Veamos cuál es el lim_n->+inf b_n - a_n.
b_n - a_n es la longitud del intervalo [a_n,b_n].
La longitud del intervalo [a₁,b₁] es (b-a)/2, la mitad de la longitud de [a,b] que es b-a.
La longitud del intervalo [a₂,b₂] es (b-a)/2², la mitad de la longitud de [a₁,b₁] que es (b-a)/2.
Y siguiendo de esta manera, la longitud del intervalo [a_n,b_n] es (b-a)/2ⁿ.

De modo que...
3) lim_n->+inf b_n - a_n = lim_n->+inf (b - a)/2ⁿ = 0.

(1), (2) y (3) son las condiciones de la definición de PSMC.
Es decir que las sucesiones a_n y b_n cumplen con la definición de PSMC:

• a_n es creciente, b_n es decreciente
• Para todo n natural a_n < b_n
• Para todo ε>0 existe n₀ natural / b_n0 - a_n0 < ε (que es lo mismo que lim_n->+inf b_n - a_n = 0.)

((a_n),(b_n)) es un PSMC y, por lo tanto, tiene frontera:
existe c / para todo n a_n <= c <= b_n, lim a_n = c- y lim b_n = c+.

lim a_n = c- significa que para todo δ > 0 existe n₁ / para todo n >= n₁ c - δ < a_n < c.
lim b_n = c+ significa que para todo δ > 0 existe n₂ / para todo n >= n₂ c < b_n < c + δ.
O sea que tomando el mayor entre n₁y n₂, llamémosle n₃, se cumplen ambas cosas. Es decir, para todo δ > 0 existe n₃ / para todo n >= n₃ c - δ < [a_n,b_n] < c + δ.

Esto significa que, para cualquier entorno de c que consideremos, existe un intervalo [an,bn] contenido en dicho entorno.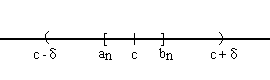

Por otro lado, f es continua en [a,b] por hipótesis. Por lo tanto es continua en c. Por definición de continuidad, lim_x->cf(x) = f(c), o sea, para todo ε > 0 existe δ > 0 / para todo x perteneciente al E^*_c,δ f(c) - ε < f(x) < f(c) + ε.

Es decir, f está acotada en 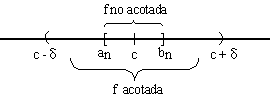(c - δ, c + δ).
Pero antes dijimos que f no estaba acotada en ninguno de los intervalos [a_n,b_n].

Tenemos pues aquí una contradicción: decimos que f está acotada en (c - δ, c + δ), pero no en [a_n,b_n] que está contenido dentro, lo cual es absurdo.

Este absurdo proviene de suponer que f no está acotada en [a,b].

Máximo y mínimo absoluto

Llamamos máximos relativos y mínimos relativos a aquellos puntos donde la función f tiene un valor máximo o mínimo comparado con los valores de f(x) para x en algún entorno de esos puntos.

Cuando hablamos de máximo y mínimo absoluto nos referimos al máximo y al mínimo de f en relación con todos los valores posibles de f(x), para todo x del dominio.

Para localizar los máximos absolutos (mínimos absolutos) de la función, debemos comparar los máximos relativos (mínimos relativos) y ver cuál de estos valores es el mayor (menor).

Teorema de Weierstrass

Una función continua en un intervalo cerrado, tiene máximo y mínimo absoluto en dicho intervalo.

H) f es continua en [a,b].
T) f tiene máximo y mínimo absoluto en [a,b].

Demostración:

Por hipótesis, f es continua en [a,b] => por el lema de Weierstrass f está acotada en [a,b], es decir, existen m y n tales que m <= f(x) <= n para todo x perteneciente a [a,b].

La demostración se realiza por reducción al absurdo.

Primero demostraremos que f tiene máximo absoluto en [a,b].
Queremos probar que existe x₁ perteneciente a [a,b] / f(x₁) = n.
Supongamos lo contrario de lo que queremos demostrar, o sea que para todo x perteneciente a [a,b] f(x) ≠ n, f(x) < n.

Sea g una función auxiliar: g(x)=1/(n - f(x)).

g es continua en [a,b] por ser diferencia y cociente de funciones continuas y n - f(x) ≠ 0. Por el lema de Weierstrass, g está acotada, es decir, para todo x perteneciente a [a,b]

s <= g(x) <= t
1/(n - f(x)) <= t
1/t <= n - f(x)
f(x) <= n - 1/t

=> n - 1/t es una cota superior de f en [a,b] (1)

Por otro lado g(x) > 0 => t > 0 => 1/t > 0 => n - 1/t < n (2)

De (1) y (2) se deduce que existe una cota superior de f menor que n, el extremo superior, lo cual es absurdo, pues el extremo superior es la menor de las cotas superiores.

El absurdo surge de suponer que no existe x tal que f(x)=n, por lo tanto existe x₁ perteneciente a [a,b] / f(x₁)=n.

Demostraremos ahora que f tiene mínimo absoluto.
Procederemos como en el caso anterior, por el absurdo.
Supondremos que para todo x perteneciente a [a,b] f(x) ≠ m, f(x) > m.

Sea h una función auxiliar: h(x) = 1/(f(x)-m)

h es continua en [a,b] por ser diferencia y cociente de funciones continuas y f(x)≠m.
Por el lema de Weierstrass, h está acotada, es decir, para todo x perteneciente a [a,b]

h <= h(x) <= k
1/(f(x)-m) <= k
1/k <= f(x) - m
f(x) >= 1/k + m

=> 1/k + m es una cota inferior de f (1)

Por otro lado h(x)>0 => k>0 => 1/k>0 => 1/k + m > m (2)

De (1) y (2) se deduce que existe una cota inferior de f mayor que el extremo inferior, lo cual es absurdo.
Este absurdo proviene de suponer que no existe x tal que f(x)=m.
Por lo tanto, sí existe algún x tal que f(x)=m.

<< anterior

Cálculo > Continuidad

Definición – Bolzano y Darboux – Weierstrass