• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Concavidad

Definición

Derivada segunda

Se llama derivada segunda de una función f(x) a la derivada de la derivada de dicha función.
Notación: f''(x).
Este concepto se puede extender a la derivada n-ésima de una función.

Definición

Ecuación de la recta tangente a una función f en x=a

La ecuación de una recta que pasa por el punto (a,f(a)) es y = m(x-a) + f(a), siendo m la tangente del ángulo que forma la recta con el eje ox.
Para obtener la ecuación de la recta tangente a f en x=a, m debe ser f'(a).

Ecuación de la tangente: y = f'(a)(x-a) + f(a)

Nota: en las siguientes definiciones y teoremas, utilizaremos el concepto de entorno de a (E_a) y entorno reducido de a (E^*_a). Para ver las definiciones, visitar la página sobre límite finito.

Definición

Concavidad

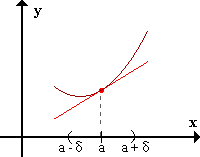
f presenta concavidad positiva en x=a si existe un E^*_a / para todo x perteneciente al E^*_a f(x) > f'(a)(x-a) + f(a).

La función presenta concavidad positiva en el punto a si, en un entorno reducido de a, la gráfica de f está "por encima" de la recta tangente a f(x) en el punto a.

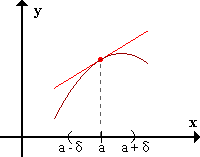
f presenta concavidad negativa en x=a si existe un E^*_a / para todo x perteneciente al E^*_a f(x) < f'(a)(x-a) + f(a).

La función presenta concavidad negativa en el punto a si, en un entorno reducido de a, la gráfica de f está "por debajo" de la recta tangente a f(x) en el punto a.

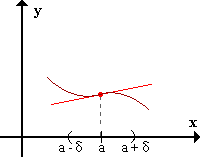
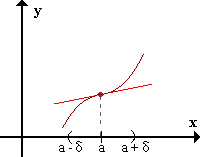
Definición

Punto de inflexión

f presenta un punto de inflexión en x=a si existe δ > 0 / para todo x perteneciente a (a - δ,a) f(x) > f'(a)(x-a) + f(a) y para todo x perteneciente a (a,a + δ) f(x) < f'(a)(x-a) + f(a) (o viceversa: f menor a la izquierda y mayor a la derecha).

		En el semientorno izquierdo de a, f está por encima de la tangente a f(x) en a, y en el semientorno derecho de a, f está por debajo de la tangente.
		En el semientorno izquierdo de a, f está por debajo de la tangente a f(x) en a, y en el semientorno derecho de a, f está por encima de la tangente.

Teorema

Condición suficiente para la existencia de concavidad positiva

Si la derivada segunda de una función f(x) es positiva en el punto a, entonces tiene concavidad positiva en dicho punto.

H) f''(a)>0
T) f tiene concavidad positiva en x=a

Demostración:

Existe f''(a) => existe f'(a) => (teorema) f es continua en x=a.

Sea g(x) = f(x) - f'(a)(x - a) - f(a)

g'(x) = f'(x) - f'(a)
g''(x) = f''(x)
g''(a) = f''(a) > 0 => por Cond. suf. para el crecimiento puntual g'(x) es creciente en x=a
=> por def. de crecimiento puntual existe δ>0 / para todo x₁ perteneciente a (a - δ,a) g'(x) < g'(a) = 0 y para todo x₂ perteneciente a (a, a + δ) g'(x) > g'(a) = 0

signo de g'(x):

   -   0   +
-------|-------
       a   

=> por Cond. suf. para la existencia de mínimo relativo g presenta un mínimo relativo en x=a.
=> por def. de mínimo relativo existe un E^*_a / para todo x perteneciente al E^*_a g(x) > g(a) = 0.
f(x) - f'(a)(x - a) - f(a) > 0
f(x) > f'(a)(x - a) + f(a) => por definición f tiene concavidad positiva en x=a.

Teorema

Condición suficiente para la existencia de concavidad negativa

Si la derivada segunda de una función f(x) es negativa en el punto a, entonces tiene concavidad negativa en dicho punto.

H) f''(a) < 0
T) f tiene concavidad negativa en x=a

La demostración es análoga a la anterior.

Teorema

Condición suficiente para la existencia de puntos de inflexión

H) La derivada segunda de f(x) es negativa en un semientorno del punto a y positiva en el otro semientorno
T) f presenta un punto de inflexión en x=a

Demostración:

Sea g(x) = f(x) - f'(a)(x - a) - f(a)

g es derivable y continua en x=a.
g'(x) = f'(x) - f'(a)
g'(a) = 0
g''(x) = f''(x) =>

signo de g''(x):

   -       +
-------|-------
       a   

=> por cond. suf. para la existencia de mínimo relativo g' presenta un mínimo relativo en a

=> por def. de mínimo relativo, existe un E^*_a / para todo x perteneciente al E*_a g'(x) > g'(a) = 0

signo de g'(x):

   +   0   +
-------|-------
       a   

=> g es creciente en a

La tangente a g en x=a es horizontal, pero igual g es creciente. La gráfica de g cerca de a es algo como

por def. de crecimiento puntual, existe δ > 0 / para todo x perteneciente a (a - δ,a) g(x) < g(a) = 0
=> f(x) - f'(a)(x-a) - f(a) < 0 => f(x) < f'(a)(x-a) + f(a)

y para todo x perteneciente a (a,a + δ) g(x) > g(a) = 0
=> f(x) - f'(a)(x-a) - f(a) > 0 => f(x) > f'(a)(x-a) + f(a)

por definición, f presenta un punto de inflexión en x=a.

Ejemplo

f(x) = x3 f'(x) = 3x2 f''(x) = 6x - 0 + sg f'' ----|----> 0 f presenta un punto de inflexión en x=0

Teorema

H) f''(x) > 0 para todo x perteneciente a [a,b]
T) Para todo x perteneciente a (a,b) f(x) < ((f(b) - f(a))/(b - a))(x - a) + f(a)

Si una función tiene concavidad positiva en un intervalo cerrado [a,b], entonces la gráfica de la función en dicho intervalo está por debajo de la recta que pasa por los puntos (a,f(a)) y (b,f(b)).

Demostración:

f''(x) > 0 para todo x perteneciente a [a,b] => por cond. suf. para el crecimiento en un intervalo f' es creciente en [a,b]

Sea x perteneciente a [a,b].
En [a,x] f es derivable => (teorema) f es continua => por teo. de Lagrange existe c perteneciente a (a,x) / f'(c) = (f(x) - f(a))/(x-a)

En [x,b] f es derivable => (teorema) f es continua => por teo. de Lagrange existe d perteneciente a (x,b) / f'(d) = (f(b) - f(x))/(b-x)

a < c < x y x < d < b => c < d => f'(c) < f'(d) pues f' es creciente en [a,b]

   f(x) - f(a)   f(b) - f(x) 
=> ----------- < -----------
      x - a         b - x

       f(b) - f(a) 
f(x) < -----------(x - a) + f(a)
          b - a     

Teorema

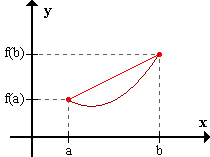
H) f''(x) < 0 para todo x perteneciente a [a,b]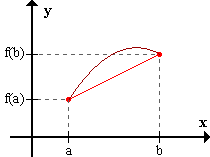
T) f(x) > ((f(b) - f(a))/(b - a))(x - a) + f(a)

Si una función tiene concavidad negativa en un intervalo cerrado [a,b], entonces la gráfica de la función en dicho intervalo está por encima de la recta que pasa por los puntos (a,f(a)) y (b,f(b)).

Demostración análoga a la anterior.

Teorema

H) f''(x) > 0 para todo x perteneciente a [a,b]
    c pertenece a (a,b)
T) f(x) > f'(c)(x-c) + f(c) para todo x perteneciente a (a,b)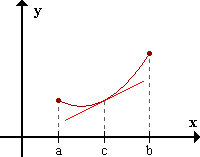

Los valores de f son mayores que las correspondientes ordenadas de la recta tangente a la curva f(x) en cualquier punto c del intervalo (a,b).

Demostración:

f''(x)>0 para todo x perteneciente a [a,b] => por Cond. suficiente para el crecimiento en un intervalo, f' es creciente en [a,b] => f' es creciente en [a,c] (1)

Sea x perteneciente a [a,c].

f es derivable en [a,x] => por teo. de Lagrange existe d perteneciente a (a,x) / f'(d) = (f(x) - f(a))/(x - a)

f es derivable en [x,c] => por teo. de Lagrange existe e perteneciente a (x,c) / f'(e) = (f(c) - f(x))/(c - x)

a < d < x < e < c => d < e => por (1) f'(d) < f'(e)

   f(x) - f(a)   f(c) - f(x)
=> ---------- <  -----------
      x - a         c - x

                            f(c) - f(a)   
Divido entre c - a: f(x) <  ----------(x - a) + f(a)
                               c - a    

Teorema

H) f continua en [a,b]
   f es derivable en (a,b)
   f'(x) distinto de 0 para todo x perteneciente a (a,b)
T) f es monótona en [a,b]

Demostración:

f continua en [a,b].
f es derivable en (a,b).
Si f(a)=f(b)

=> por teo. de Rolle existe c perteneciente a (a,b) / f'(c)=0.
Absurdo => f(a)≠f(b)

Si f(a) < f(b):

Sea x₁ perteneciente a (a,b).
Supongamos f(a) > f(x₁) (1)

Considero [x₁,b].

• f es continua en [x₁,b]
  
• f(x₁) < f(a) < f(b)

=> por la propiedad de Darboux existe x₂ perteneciente a (x₁,b) / f(x₂) = f(a)

Considero [a,x₂]

• f continua y derivable en (a,x₂)
  
• f(a) = f(x₂)

=> por teo. de Rolle existe x₃ perteneciente a (a,x₂) / f'(x₃) = 0. Absurdo que proviene de (1).

Sea x₄ perteneciente a (a,b)
Supongamos f(x₄) > f(b) (2)

• f es continua en [a,x₄]
  
• f(x₄) > f(b) > f(a)

=> por la propiedad de Darboux existe x₅ perteneciente a (a,x₄) / f(x₅) = f(b)

• f continua y derivable en [x₅,b]
  
• f(x₅) = f(b)

=> por teo. de Rolle existe x₆ perteneciente a (x₅,b) / f'(x₆) = 0. Absurdo de (2).

=> Para todo x perteneciente a (a,b) f(a) < f(x) < f(b)

Sean x₇ y x₈ pertenecientes a (a,b)
x₇ < x₈.
Supongamos f(x₇) > f(x₈) (3)

• f(a) < f(x₈) < f(x₇)
• f continua en [a,x₇]

=> por la propiedad de Darboux existe x₉ perteneciente a (a,x₇) / f(x₉) = f(x₈)

• f continua y derivable en [x₉,x₈]
  
• f(x₉) = f(x₈)

=> por teo. de Rolle existe x₁₀ perteneciente a (x₉,x₈) / f'(x₁₀) = 0. Absurdo de (3).

=> por def. de función monótona creciente en un intervalo f es monótona creciente en [a,b]

(Si suponemos f(a) > f(b) se demuestra que f es monótona decreciente en [a,b].)

<< anterior  siguiente >>

Cálculo > Variación

Crecimiento – Concavidad – Función inversa