Comenzar un plan no es poco, y en ocasiones es mucho.
Sócrates.
 















Existencia y continuidad de la función inversa

Sea f una función que asocia a un punto x de su dominio la imagen y=f(x). Supongamos que f es tal que diferentes x son transformados siempre en diferentes y. Así, cada y en el rango de f es la imagen de a lo más un valor x. Puede asociarse con cada y en el rango de f el valor x que es su preimagen. De esta manera, se define una función g cuyo dominio es el rango de f y que al aplicarse a una imagen y=f(x), reproduce el valor original x, esto es, g(f(x))=x.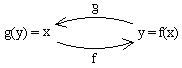
g se denomina la inversa de f y se denota f-1. Esta función g se halla al despejar la x en función de y.
f también es la inversa de g, de modo que también f(g(y))=y.

Si la función g se representa de la manera usual, como función de x, por y=g(x), entonces la gráfica de y=g(x) es simétrica de la gráfica de y=f(x) con respecto a la recta y=x.

Ejemplo:

y=f(x)=ex

Despejando x en función de y: x = Ly
Por lo tanto, f-1(y) = Ly
Expresando f-1 en función de x: f-1(x) = Lx

Funciones inversas: e^x y Lx    La gráfica de f(x) es simétrica de la gráfica de f-1(x) con respecto a la recta y=x.

Para que exista la inversa de una función f, f debe ser biyectiva.

Revisaremos las definiciones de función inyectiva, biyectiva y sobreyectiva:

Inyectiva: a cada elemento del dominio le corresponde sólo un elemento del codominio, pero pueden existir elementos del codominio que no tengan correspondiente en el dominio.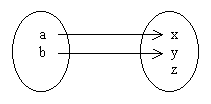

Biyectiva o biunívoca o "uno a uno": a cada elemento del dominio le corresponde un sólo elemento del codominio y a cada elemento del codominio le corresponde un sólo elemento del dominio.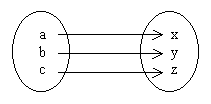

Sobreyectiva: a cada elemento del dominio le corresponde un sólo elemento del codominio y a cada elemento del codominio le corresponde por lo menos un elemento del dominio.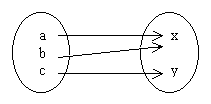

Es condición necesaria y suficiente para que la inversa de una función f sea otra función que f sea biyectiva.

f-1 es una función <=> f es biyectiva

Demostraremos a continuación que, si una función f es continua y monótona en un intervalo [a,b], entonces existe la inversa en [f(a),f(b)], y es también monótona y continua.

Teorema

H) f continua en [a,b]
    f creciente o decreciente en [a,b]
T) El recorrido de f en [a,b] es [f(a),f(b)]
    Existe f-1 en [f(a),f(b)]
    f-1 es creciente o decreciente
    f-1 es continua en [f(a),f(b)]

Demostración:

Supongamos f creciente en [a,b]

  1. Sea x perteneciente a [a,b] => a <= x <= b => f(a) <= f(x) <= f(b) pues f es creciente => f(x) pertenece a [f(a),f(b)]

    Sea z perteneciente a [f(a),f(b)] =>

    • f(a) <= z <= f(b)
    • f continua en [a,b]

    => De 1) y 2) por la propiedad de Darboux existe c perteneciente a (a,b) / f(c)=z.

  2. Debemos probar que f es biyectiva.

    Sean x1 y x2 pertenecientes a [a,b], x1 < x2

    => f(x1) < f(x2) pues f es creciente en [a,b] => f no es sobreyectiva.

    De 1) para todo z perteneciente a [f(a),f(b)] existe x0 perteneciente a (a,b) / f(x0)=z => f no es inyectiva => f es biyectiva.

  3. Sean z1 y z2 pertenecientes a [f(a),f(b)], z1 < z2.

    Supongo f-1(z1) > f-1(z2) => como f es creciente f(f-1(z1)) > f(f-1(z2)) o sea z1 > z2. Absurdo.

    Supongo f-1(z1) = f-1(z2) => f(f-1(z1)) = f(f-1(z2)) o sea z1 = z2. Absurdo.

    => f-1(z1) < f-1(z2) => f-1 es creciente.
    (Si f es decreciente, f-1 es decreciente.)

  4. Sea z0 perteneciente a (f(a),f(b)) => por 2) existe f-1(z0) y f-1(z0) pertenece a (a,b). Existe un Ef-1(z0) contenido en [a,b]

    a < f-1(z0) - ε < f-1(z0) < f-1(z0) + ε < b

    Aplico f: f(a) < f[f-1(z0) - ε] < z0 < f[f-1(z0) + ε] < f(b)

    f(a) < k < z0 < k' < f(b)

    [k,k'] = Ez0
    Para todo x / k < x < k' f-1(x) pertenece a un Ef-1(z0),ε

    => para todo z0 perteneciente a (f(a),f(b)) limx->z0 f-1(x) = f-1(z0)


<< anterior

Página principal

Tabla de Contenidos

Noticias matemáticas
 
Cálculo > Variación
Crecimiento – Concavidad – Función inversa

Última modificación: noviembre 2004
Página principal     Tabla de contenidos     E-mail