
La repetición es la madre de la habilidad.
Mr. Shoaff.
 |
La repetición es la madre de la habilidad. Mr. Shoaff. |
Operaciones con límitesTeoremaLímite de la suma
El límite de una suma es igual a la suma de los límites de cada término, siempre
que estos límites sean finitos.
Queremos probar que, dado Sea ε' = ε/2
limx->af(x)=b => (por def. de límite) para todo
limx->ag(x)=c => (por def. de límite) para todo Sea δ = min {δ1,δ2} Para todo x perteneciente al E*a,δ se cumple:
=> |f(x) - b| + |g(x) - c| < 2ε' = ε
|(f(x) + g(x)) - (b+c)| = |(f(x) - b) + (g(x) - c)| <= (*) (*) Desigualdad triangular: |a + b| <= |a| + |b| => (por def. de límite) limx->af(x) + g(x) = b + c Ejemplo:
limx->2 x2 = 4 Teorema
H) limx->af(x) = b, limx->ag(x) = +inf
limx->af(x)=b => (por def. de límite) para todo Eb,ε existe un E*a,δ1
/ para todo x perteneciente al E*a,δ1
limx->ag(x)= +inf => (por def. de límite infinito) para todo A > 0 existe un E*a,δ2
/ para todo x perteneciente al E*a,δ2 Sea δ = min {δ1,δ2} Para todo x perteneciente al E*a,δ se cumple:
=> f(x) + g(x) > A + b - ε = K => (por def. de límite infinito) limx->a f(x) + g(x) = +inf. Teorema
H) limx->af(x) = b, limx->ag(x) = -inf Análoga a la anterior. Teorema
H) limx->af(x) = +inf, limx->ag(x) = +inf
Sea A > 0.
Por def. de límite infinito, existe δ1 > 0 / para todo x perteneciente al E*a,δ1
Por def. de límite infinito, existe δ2 > 0 / para todo x perteneciente al Sea δ = min {δ1,δ2} Para todo x perteneciente al E*a,δ f(x) + g(x) > A => (por def. de límite infinito) limx->af(x) + g(x) = +inf. Teorema
H) limx->af(x) = -inf, limx->ag(x) = -inf Análoga a la anterior. Cuando limx->af(x) = -inf y limx->ag(x) = +inf, el limx->af(x) + g(x) no puede determinarse, se dice que es INDETERMINADO de la forma inf - inf. TeoremaLímite del producto
H) limx->af(x) = b, limx->ag(x) = c
Queremos probar que, dado ε > 0, existe δ > 0 / para todo x perteneciente al E*a,δ
limx->af(x) = b => (por def. de límite) para todo Eb,ε1 existe E*a,δ1 / para todo x perteneciente al E*a,δ1 f(x) pertenece al Eb,ε1. limx->ag(x) = c => (por def. de límite) para todo Ec,ε2 existe E*a,δ2 / para todo x perteneciente al E*a,δ2 f(x) pertenece al Ec,ε2.
limx->af(x) = b => (por teo. de la acotación) existe δ3 > 0 y k > 0 / para todo
x perteneciente al E*a,δ3
ε ε
Sea ε1 = --- , ε2 = ---
2|c| 2k
ε ε
|f(x) - b| < --- => |c||f(x) - b| < --- (1)
2|c| 2
ε ε
|g(x) - c| < --- => k|g(x) - c| < --- (2)
2k 2
ε
|f(x)| < k => (de 2) |f(x)||g(x) - c| < --- (3)
2
Sea δ = min {δ1,δ2}
De 1) y 3): para todo x perteneciente al |c||f(x) - b| + |f(x)||g(x) - c| < ε |f(x)g(x) - bc| = |f(x)g(x) - bc + f(x)c - f(x)c| = |c(f(x) - b) + f(x)(g(x) - c)| <= (*) |c||f(x) - b| + |f(x)||g(x) - c| < ε (*) Desigualdad triangular: |a + b| <= |a| + |b| => |f(x)g(x) - bc| < ε => (por def. de límite) limx->af(x)g(x) = bc Ejemplo
limx->2 x = 2 Teorema
H) limx->af(x) = b, limx->ag(x) = inf Nota: inf denota el infinito, positivo o negativo.
Caso 1:
Caso 2:
Caso 3:
Caso 4:
Quiero probar que para todo B > 0 existe δ > 0 / para todo x perteneciente al
E*a,δ
limx->af(x) = b => (por teo. de la acotación) existe
limx->ag(x) = +inf => (por def. de límite infinito) para todo A > 0 existe
Sea δ = min {δ1,δ2} Para todo x perteneciente al E*a,δ
=> f(x)g(x) > kA > B Los demás casos se demuestran en forma análoga. Si b = 0 el limx->af(x)g(x) no puede determinarse. Se dice que es una INDETERMINACIóN de la forma 0.inf. TeoremaLímite del cociente
H) limx->af(x) = b, limx->ag(x) = c (c distinto de 0)
limx->af(x) = b => (por def. de límite) para todo Eb,ε1 existe
un E*a,δ1 / para todo x perteneciente al E*a,δ1
limx->ag(x) = c => (por def. de límite) para todo Ec,ε2 existe
un E*a,δ2 / para todo x perteneciente al E*a,δ2
Quiero probar que limx->af(x)/g(x) = b/c, o sea que para todo Eb/c,ε existe un E*a,δ / para todo x perteneciente al E*a,δ |f(x)/g(x) - b/c| < ε.
|f(x)c - g(x)b| |f(x)c - g(x)b - bc + bc|
|f(x)/g(x) - b/c| = --------------- = ------------------------- =
|g(x)c| |g(x)c|
|c(f(x) - b) + b(c - g(x))| |c||f(x) - b| + |b||c - g(x)|
--------------------------- <= ----------------------------- <
|g(x)c| (*) |g(x)c| (**)
|c||f(x) - b| + |b||c - g(x)| (1)
-----------------------------
k|c|
(*) Desigualdad triangular: |a + b| <= |a| + |b|. (**) pues |g(x)|> h por teo. de la acotación. Sea ε1 = εh/2 y ε2 = εh|c|/2|b| Para todo x perteneciente al E*a,δ1
|f(x) - b| < εh |c||f(x) - b| < εh|c| (2)
--- => ----
2 2
Para todo x perteneciente al E*a,δ2
|g(x) - c| < εh|c| |b||g(x) - c| < εh|c| (3)
----- => ----
2|b| 2
Sea δ = min {δ1,δ2} De 2) y 3): para todo x perteneciente al E*a,δ
|c||f(x) - b| + |b||c - g(x)| εh|c|
=> |f(x)/g(x) - b/c| < ----------------------------- < ----- = ε
por 1) h|c| h|c|
Ejemplo
ex 1
lim ----- = --
x->0 x + 2 2
Otros cocientes
Caso 1:
El límite 0+ indica que, en un entorno de a, f(x) se aproxima a 0 por la derecha,
es decir,
Caso 2:
Caso 3:
Caso 4:
Si limx->af(x) = 0 y limx->ag(x) = 0, limx->af(x)/g(x) no puede
determinarse. Se dice que es INDETERMINADO de la forma 0/0. Límite exponencial
Caso 1:
Caso 2:
Caso 3:
Caso 4:
Si limx->af(x) = 0 y limx->ag(x) = inf, limx->af(x)g(x) no puede
determinarse. Se dice que es INDETERMINADO de la forma 0inf. Teorema
H) limx->a f(x) = 1, limx->a g(x) = inf Sea h(x) = f(x) - 1 lim h(x) = 0 por límite de la suma f(x) = 1 + h(x)
lim (1 + h(x))g(x) = lim (1 + h(x))g(x).(h(x)/h(x)) =
h(x)->0, g(x)->inf h(x)->0, g(x)->inf
h(x)≠0
e
-------^------- (1)
lim (1 + h(x))1/h(x).g(x).h(x) = elim g(x).h(x) =
h(x)->0, g(x)->inf
h(x)≠0
lim g(x)(f(x) - 1)
e g(x)->inf, f(x)->1
1) por límite tipo 2 y límite exponencial. Función compuesta
Si f es una función tal que f:A->B y g es una función tal que g:C->D, y B es subconjunto de C
(el dominio de g contiene al rango de f), podemos definir una nueva función h:A->D como sigue:
para cada x en A, se aplica f resultando un valor f(x) en B. Luego a este valor f(x) se aplica g,
obteniéndose g[f(x)]. Definimos h como la función que mapea x en g[f(x)]. Se dice que h
es la composición de g y f: 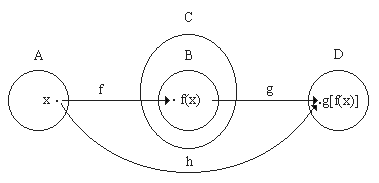
TeoremaLímite de la función compuesta
H) limx->af(x)=b, limx->bg(x)=c Queremos demostrar que limx->a g[f(x)]=c, o sea, por definición de límite, queremos probar que, dado ε>0 existe δ>0 tal que para todo x perteneciente al E*a,δ g[f(x)] perteneciente al Ec,ε. Por hipótesis limx->bg(x)=c => por def. de límite, dado ε>0 existe δ>0 tal que... para todo x perteneciente al E*b,δ g(x) pertenece al Ec,ε (1) Por hipótesis limx->af(x) = b => por def. de límite si tomamos el número δ de (1), existe α>0 tal que... para todo x perteneciente al E*a,α f(x) pertenece al Eb,δ (2)
De (1) y (2) se deduce que: 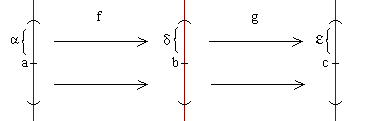
|
Página principal Tabla de Contenidos Noticias matemáticas |
|||||
|
||
|
Última modificación: noviembre 2004 Página principal Tabla de contenidos E-mail |