• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Métodos de aproximación de raíces

Cuando se trata de hallar las raíces de una función f(x), se debe resolver la ecuación f(x)=0. En algunos casos, esto es una tarea sencilla, por ejemplo con las funciones lineales o cuadráticas, pero en otros no es nada fácil. Para estos casos, existen métodos útiles que permiten, si no determinar, aproximar las raíces buscadas.

Método de Rolle

Se halla la derivada primera y luego se estudian sus ceros y su signo.

Por ejemplo, si el signo de f'(x) es

  -  0  +  0  -
-----|-----|----->
     a     b  

En el intervalo (a,b) la función es creciente (ver condición suficiente para el crecimiento en un intervalo).
Si el signo de f en a y b es el mismo (positivo o negativo), f no cruza el eje ox en (a,b).
Si el signo de f en a es distinto del signo de f en b, entonces por el teorema de Bolzano, f tiene una raíz en (a,b), y es una sola por ser creciente.
Para hallar esa raíz se va partiendo el intervalo hasta que se llega a ella o a una aproximación.

Veámoslo más claramente con un ejemplo.

f(x) = 2x³ + 3x² - 12x - 30

f'(x) = 6x² + 6x - 12

         +   0   -   0   +
sg f' -------|-------|------->
            -2       1

f(-2) = -10

f(1) = -37

      -inf   -       -   +inf
sg f  -------|-------|------->
            -2       1   

f es decreciente en (-2,1) (ver signo de f') y negativa en los extremos (ver signo de f) => no tiene raíz en ese intervalo.

f es creciente en (1,+inf), de acuerdo al signo de f', y como es negativa en 1 y positiva para valores muy grandes de x, tiene una raíz α > 1.

f(2) = -26
f(3) = 15
=> 2 < α < 3

Probemos entonces con 2.5:
f(2.5) = -10
=> 2.5 < α < 3

Probemos con 2.8:
f(2.8) = 3.824
=> 2.5 < α < 2.8

Veamos f(2.7):
f(2.7) = -1.164
=> 2.7 < α < 2.8

Continuando de esta manera, llegamos a que α está entre 2.72 y 2.73:
f(2.73) = 0.29
f(2.72) = -0.19

=> Podemos aproximar α a 2.725.
Si quisiéramos una aproximación mayor de la raíz, deberíamos seguir este proceso.

Método de Ábacos

Se utiliza cuando la función puede expresarse como diferencia de dos funciones fáciles de graficar.

Veamos un ejemplo:

f(x) = L|x| + x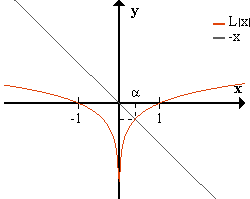
f(x) puede expresarse como f(x) = L|x| - (-x)
Graficamos sobre el mismo sistema de ejes ambas funciones: g(x) = L|x| y h(x) = -x.

En el punto donde se cortan las curvas, ambas funciones tienen el mismo valor numérico, g(α) = h(α).

Entonces α es un cero de f(x), pues f(α) = g(α) - h(α) = 0

Para valores menores que α, la recta correspondiente a -x está por encima de la curva correspondiente a L|x|, así que la resta da negativo.
Para valores de x mayores que α, L|x| es mayor que -x, así que la resta da positivo. Observando la gráfica vemos que α está entre 0 y 1.

                -  E  -  0  +  +  +  
signo de f(x) -----|-----|-----|----->
                   0     α     1 

Comencemos a aproximar:

       ~                      ~
f(0.5) = -0.19 |      f(0.56) = -0.02 |       ~
       ~       |  =>          ~       |  => α = 0.565
f(0.6) = 0.089 |      f(0.57) = 0.008 |  

siguiente >>

Cálculo > Análisis y representación

Descripción – Aproximación de raíces – Ejercicios