• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Estudio analítico y representación gráfica de f(x) = e^x(1-x) - 1.

Para conocer los detalles del procedimiento que seguiremos, ir a la página sobre estudio analítico y representacion gráfica de funciones.

1. Dominio

   f(x) no tiene ningún denominador, ninguna raíz y ningún logaritmo, por lo tanto existe para todo x real.

   Dominio de f: R

2. Continuidad y asíntotas verticales

   f(x) es continua para todo x real.

3. Ceros y signo

   Debemos resolver la ecuación f(x)=0.
   Es decir, debemos resolver
   
   e^x(1-x) = 1 => e^x = 1 y 1 - x = 1 => x = 0
   
   La única raíz de la función es 0.
   
   Para determinar el signo de f a izquierda y derecha de 0, simplemente evaluamos f en algún punto de esos intervalos, como 1 y -1.

           -   0   - 
   sg f -------|------->
               0
   

4. Asíntotas horizontales y oblicuas

                              0 por órdenes de infinitos
               IND. 0.inf   --^--        
                   |        (1-x)      
   lim ex(1-x) - 1 = lim    ----- - 1 = -1
   x->-inf           x->-inf 1/ex      
   

   Asíntota horizontal y=-1 para x->-inf

   lim f(x) = -inf
   x->+inf                                              
                                            -1      0+
                                     +inf  --^--   -^-      
         f(x)       ex(1-x) - 1       -^-  (1-x)    1
   lim   ---- = lim ----------- = lim  ex. ----- - --- =        
   x->+inf x    x->+inf   x       x->+inf    x      x
   
   = -inf    
   

   DA || oy para +inf

   Comencemos a representar la información obtenida hasta ahora:

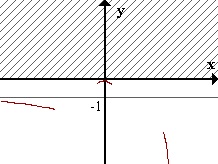
   Tachamos el área por encima del eje ox, pues f es negativa, salvo en x=0 donde vale 0. Asíntota horizontal y=-1 para x->-inf. DA paralela al eje oy para +inf.

5. Derivada primera

   f'(x) = e^x(1-x) - e^x = -xe^x

        
           +  0  -
   sg f' -----|----->      
              0
            máximo	        
   

   f(0) = 0
   Máximo en (0,0)

6. Derivada segunda

   f''(x) = -e^x - xe^x = -e^x(x+1)

            +  0  -  
   sg f'' -----|----->
              -1  
         	punto de inflexión	   
                   ~
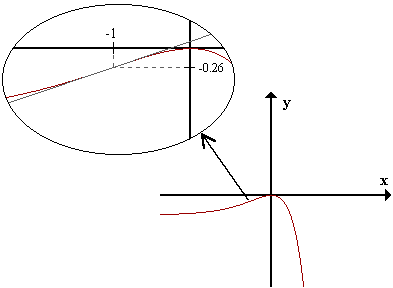
   f(-1) = 2/e - 1 = -0.26
   
   

   Punto de inflexión en (-1, -0.26)

   Tangente en el punto:
   y = f'(-1)(x+1) + f(-1) = 1/e(x+1) + 2/e - 1 = (1/e)x + 3/e - 1

   Máximo en (0,0) Punto de inflexión en (-1,-0.26) Tangente: y = (1/e)x + 3/e - 1

Veamos la gráfica exacta de la función para compararla con nuestra representación:

siguiente >>

Cálculo > Análisis y representación > Ejercicios

f(x) = e^x(1-x) - 1
f(x) = |x-2|e^{(1 + sg x)x/2}
f(x) = L²|x| - (x-1)²/2
f(x) = 2L(1+x) - x/(1+x)
f(x) = Lx + L|x-1| + (x²+1)/2 - 2x + 1
f(x) = |xL|x|| - |1-x²|/4
f(x) = (2L|x| + 1)/(L|x| + 1) - x/4e