• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos
• Primos de Mersenne

Teoremas sobre límites

Teorema

Si una función tiene límite es único.

H) Existe lim_x->af(x)=b
T) b es único

La demostración se hace por reducción al absurdo.
Suponemos que f(x) tiene dos límites distintos b y c, cuando x tiende a a.
Suponemos que b > c.

lim_x->af(x)=b => (por def. de límite) para todo E_b,ε existe un E^*_a,δ1 / para todo x perteneciente al E^*_a,δ1 f(x) pertenece al E_b,ε.

lim_x->af(x)=c => (por def. de límite) para todo E_c,ε existe un E^*_a,δ2 / para todo x perteneciente al E^*_a,δ2 f(x) pertenece al E_c,ε.

Consideremos un ε tal que 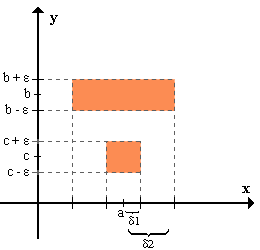E_b,ε ∩ E_c,ε = Ø.

Queremos que c+ε < b-ε => ε < (b - c)/2

Sea δ = min {δ1,δ2}

Para todo x perteneciente al E^*_a,δ se cumple

• f(x) pertenece a E_b,ε
• f(x) pertenece a E_c,ε

Absurdo, pues f(x) no puede pertenecer a dos entornos disjuntos.
Absurdo de suponer b ≠ c.
Por lo tanto b = c.

Definición

Límite de f(x) en el punto a por la derecha :
lim_x->a+f(x)=b <=> para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a,a + δ) |f(x) - b| < ε.
Límite de f(x) en el punto a por la izquierda :
lim_x->a-f(x)=b <=> para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a - δ,a) |f(x) - b| < ε.

Nota: x->a+ indica que x tiende a a por la derecha, es decir que x pertenece al entorno (a,a + δ).
x->a- indica que x tiende a a por la izquierda, es decir que x pertenece al entorno (a - δ,a).

A veces las funciones son discontinuas o no están definidas en un punto a, pero son continuas a uno y otro lado. En estos casos, el límite por la izquierda puede ser distinto del límite por la derecha.

Ejemplo

f(x) =  x2 si x <= 2
        -2x + 1 si x > 2

limx->2-f(x)=4 limx->2+f(x)=-3 No existe limx->2f(x)

Teorema

Existe el límite finito de una función <=> los límites laterales son iguales.

H) lim_x->af(x)=b
T) lim_x->a+f(x) = lim_x->a-f(x) = b

Directo:
lim_x->af(x)=b => (por def. de límite) para todo ε > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δ f(x) pertenece al E_b,ε.

=> para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a - δ,a) f(x) pertenece al E_b,ε => (por def. de límites laterales) lim_x->a-f(x)=b.

y para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a,a + δ) f(x) pertenece al E_b,ε => (por def. de límites laterales) lim_x->a+f(x)=b.

Recíproco:
lim_x->a+f(x)=b => (por def. de límites laterales) para todo ε > 0 existe δ1 > 0 / para todo x perteneciente a (a,a + δ1) f(x) pertenece al E_b,ε.

lim_x->a-f(x)=b => (por def. de límites laterales) para todo ε > 0 existe δ2 > 0 / para todo x perteneciente a (a - δ2,a) f(x) pertenece al E_b,ε.

Sea δ = min {δ1,δ2}

Para todo x perteneciente a E^*_a,δ f(x) pertenece al E_b,ε.

=> (por def. de límite) lim_x->af(x) = b.

Ejemplo: en la función del ejemplo anterior, no existe lim_x->2f(x), pues lim_x->2-f(x) ≠ lim_x->2+f(x).

Conservación del signo

Para valores de x suficientemente próximos al valor de tendencia, la función tiene el mismo signo que su límite.

H) lim_x->af(x)=b > 0
T) Existe δ > 0 / para todo x perteneciente al E^*_a,δ f(x) > 0

lim_x->af(x)=b => (por def. de límite) para todo ε > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δ f(x) pertenece al E_b,ε.
Es decir, b - ε < f(x) < b + ε.

Consideremos ε < b => 0 < b - ε < f(x) => f(x) > 0.

Así, basta considerar un ε menor que b, para tener un entorno de a donde f(x) es mayor que 0.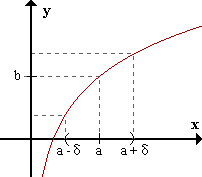

Nota: El teorema también se cumple para valores negativos.
Si la función tiene distinto signo en la mitad izquierda del entorno de a que en la mitad derecha, entonces su límite en a vale 0.

Teorema de la función comprendida

Si una función está comprendida entre otras dos que tienen igual límite cuando x tiende a a, entonces tiene el mismo límite.

H) lim_x->af(x) = lim_x->ag(x) = b
Existe δ1 > 0 / para todo x perteneciente al E^*_a,δ1 f(x) <= h(x) <= g(x)
T) lim_x->ah(x)=b

lim_x->af(x)=b => (por def. de límite) para todo ε > 0 existe δ2 > 0 / para todo x perteneciente al E^*_a,δ2 b - ε < f(x) < b + ε.

lim_x->ag(x)=b => (por def. de límite) para todo ε > 0 existe δ3 > 0 / para todo x perteneciente al E^*_a,δ3 b - ε < g(x) < b + ε.

Sea δ = min {δ1,δ2,δ3}

Para todo x perteneciente al E^*_a,δ b - ε < f(x) <= h(x) <= g(x) < b + ε

=> (por def. de límite) 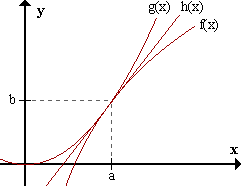lim_x->ah(x) = b.

Teorema de la acotación

Si una función tiene límite finito cuando x tiende a a, entonces está acotada en un entorno reducido de a.

H) lim_x->af(x)=b
T) Existe δ > 0 y existen h y k reales / para todo x perteneciente al E^*_a,δ h < f(x) < k

lim_x->af(x)=b => (por def. de límite) para todo ε > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δ

  b - ε  <  f(x)  <  b + ε
  --^--              --^--
    h                  k    
cota inferior      cota superior

Nota: también podemos expresar la tesis como:
Existe δ>0 y existen h y k reales positivos / para todo x perteneciente al E^*_a,δ
h < |f(x)| < k.

<< anterior  siguiente >>

Cálculo > Límites

Límite finito – Teoremas – Límite infinito – Operaciones con límites – Límites de polinomios – Límites tipo – Infinitésimos – Infinitos – Cálculo de límites – Ejercicios