|
|
|
Estudio analítico y representación gráfica de f(x) = 2L(1+x) - x/(1+x).
Para conocer los detalles del procedimiento que seguiremos, ir a la página sobre
estudio analítico y representacion gráfica de funciones.
Dominio
El logaritmo está definido para argumentos mayores que 0, es decir, para x mayores
que -1, y el denominador (1+x) no está definido en x=-1.
Dominio de f: {x/x pertenece a R ^ x>-1}
Continuidad y asíntotas verticales
(IND. 0.inf que se resuelve
por órdenes de infinitos)
0
-inf -inf -----^-----
---^--- ---^--- 2(1+x)L(1+x) - x 1
lim 2L(1+x) - x/(1+x) = lim ---------------- = --- = +inf
x->-1+ | x->-1+ 1+x 0+
|
(IND. inf-inf)
=> AV x=-1
Ceros y signo
Pasaremos por alto este paso pues la ecuación f(x)=0 es difícil de resolver.
Utilizaremos el método de Rolle para aproximar las raíces, luego
de que contemos con la información de los ceros y el signo de la derivada primera.
Asíntotas horizontales y oblicuas
1
---^---
lim 2L(1+x) - x/(1+x) = +inf
x->+inf
0 0
---^--- -^-
2L(1+x) x
lim ------- - --- = 0 => DA || ox
x->+inf x 1+x
|
|
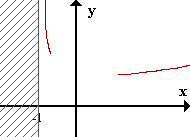
Dominio de f: x>-1.
AV x=-1.
DA paralela al eje ox para x->+inf.
|
Derivada primera
2 (1+x-x) 2x+1
f'(x) = ---- - ------- = ------
1+x (1+x)2 (1+x)2
E - 0 +
sg f' -/-/-/-/-|-----|----->
-1 -1/2
min
f(-1/2) = -0.39
Mínimo en (-0.5, -0.39)
Ceros y signo
f es negativa en -1/2
f tiende a +inf cuando x->+inf, así que es positiva para x grandes.
f tiende a +inf cuando x->-1+, así que es positiva a la derecha de -1.
Coloquemos esta información sobre un eje:
E + - +
sg f -/-/-/-/-|-----|----->
-1 -1/2
Como f es decreciente en (-1,-1/2), tiene exactamente una raíz en ese intervalo.
f es creciente para x mayores que -1/2, así que tiene exactamente una raíz mayor que -1/2.
E + 0 - - - 0 +
sg f -/-/-/-/-|---|---|---|--->
-1 α -1/2 β
Trataremos de hallar o aproximar α y β:
~
f(-0.7) = -0.075 | ~
~ > α = -0.75
f(-0.8) = -1.17 |
f(0)=0 => β = 0
Derivada segunda
2(1+x)2 - (2x+1)2(1+x) (1+x)[2(1+x) - 2(2x+1)]
f''(x) = --------------------- = ----------------------- =
(1+x)4 (1+x)4
-2x
-----
(1+x)3
E + 0 -
sg f'' -/-/-/-/-|-----|----->
-1 0
PI
f(0) = 0
f'(0) = 1
Punto de inflexión en (0,0).
Tangente en el punto: y = x.
|
|
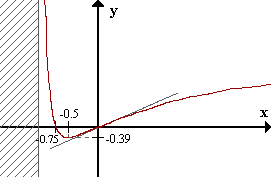
Raíces: -0.75 y 0.
Mínimo en (-0.5, -0.39).
Punto de inflexión en (0,0).
- Tangente en el punto: y=x.
|
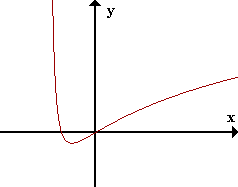
Finalmente, verifiquemos nuestro análisis observando la gráfica precisa de la función:
<< anterior siguiente >>
|
|
Página principal
Tabla de Contenidos
Noticias matemáticas
|


