|
|
|
Estudio analítico y representación gráfica de f(x) = |xL|x|| - |1-x2|/4.
Para conocer los detalles del procedimiento que seguiremos, ir a la página sobre
estudio analítico y representacion gráfica de funciones.
f es una función par, es decir f(-x)=f(x).
La gráfica de f para valores negativos de x es simétrica de la gráfica
de f para valores positivos, con respecto al eje oy.
Por lo tanto, será suficiente estudiar la función para x > 0.
Entonces podemos eliminar el valor absoluto de L|x| y trabajar con
f(x) = |xLx| - |1-x2|/4.
Para simplificar más el estudio de f, vamos a eliminar el valor absoluto de
|1-x2|.
Para ello, veamos cómo está definida la expresión |1-x2|.
| x2-1 si x < -1
|1-x2| = | 1-x2 si -1 < x < 1
| x2-1 si x > 1
Es decir que f nos queda expresada como:
f1(x) = |xLx| - (1-x2)/4 si 0 < x < 1
f2(x) = |xLx| - (x2-1)/4 si x > 1
Todavía podemos simplificar f eliminando el valor absoluto de |xLx|.
E - 0 +
sg xLx |-----|----->
0 1
Por lo tanto |xLx| puede definirse como sigue:
| -xLx si x < -1
|xLx| = |
| xLx si x > 1
Entonces f nos queda expresada como:
f1(x) = -xLx - (1-x2)/4 si 0 < x < 1
f2/(x) = xLx - (x2-1)/4 si x > 1
Dominio
L|x| no está definido en x=0 y |1-x2| no está definido en x=-1 ni en x=1.
Dominio de f: R - {-1,0,1}
Continuidad y asíntotas verticales
Lx
lim -xLx - (1-x2)/4 = lim ---- - 1/4 = -1/4
x->0+ x->0+ 1/x
lim f(x) = -1/4
x->0-
En x=0 discontinuidad evitable => f(0)=-1/4.
lim xLx - (x2-1)/4 = 0.
x->1+
lim f(x) = 0
x->1-
En x=1 discontinuidad evitable => f(1)=0.
En x=-1 los límites laterales son exactamente iguales a los calculados para x=1, así
que en x=-1 también hay una discontinuidad evitable => f(-1)=0.
Ceros y signo
Pasaremos por alto este paso pues la ecuación f(x)=0 es difícil de resolver.
Utilizaremos el método de Rolle para aproximar las raíces, luego de
que contemos con la información de los ceros y el signo de la derivada primera.
Asíntotas horizontales y oblicuas
+inf -inf
-^- --^--
x(4Lx - x) + 1
lim xLx - (x2-1)/4 = lim -------------- = -inf
x->+inf x->+inf 4
0
xLx x2 - 1 --^--
lim --- - -------- = lim Lx - x2/4x + 1/4x = lim Lx - x/4
x->+inf x 4x x->+inf x->+inf
= -inf
DA || oy
|
|
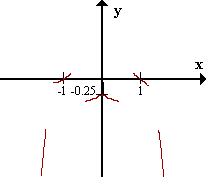
En x=-1 discontinuidad evitable: f(-1)=0.
En x=0 discontinuidad evitable: f(0)=-0.25.
En x=1 discontinuidad evitable: f(1)=0.
DA || oy para x->-inf y x->+inf.
|
Derivada primera
f'1(x) = -Lx - x/x + 2x/4 = -Lx + x/2 - 1 (x<1)
f'2(x) = Lx + x/x - 2x/4 = Lx - x/2 + 1 (x>1)
Para determinar las raíces de la derivada primera emplearemos el
método de Rolle,
luego de hallar la derivada segunda.
Derivada segunda
f''1(x) = -1/x + 1/2 (x<1)
f''2(x) = 1/x - 1/2 (x>1)
E - E + 0 -
sg f'' -/-/-/-/-/-|-------|-------|------->
0 1 2
PI
Ahora estudiaremos el signo de f'.
lim f'2(x) = -inf
x->+inf
lim f'1(x) = +inf
x->0+
lim f'1(x) = -1/2 > 0
x->1-
lim f'2(x) = 1/2 > 0
x->1+
f'2(2) = L2 > 0
E + 0 - E + + 0 -
sg f' -/-/-/-/-/-|----|----|----|----|---->
0 α 1 2 β
~ ~
Aproximando, α = 0.45 y β = 5.35
~
f(0.45) = 0.16
Máximo en (0.35,-0.37).
~
f(5.35) = 2.07
Máximo en (5.35,2.07).
f(1) = 0
Punto singular en (1,0).
lim f'1(x) = -1/2
x->1-
lim f'2(x) = 1/2
x->1+
(1,0) es un punto anguloso.
y = 1/2(x-1) = (1/2)x - 1/2 semitangente por la derecha.
y = -1/2(x-1) = (-1/2)x + 1/2 semitangente por izquierda.
f(2) = L2
(2,L2) punto de inflexión.
f'(2) = L2
tangente en PI: y = L2(x-2) + L2 = L2x - L2
Ceros y signo
E + 0 - E + + 0 -
sg f' |----|----|----|----|---->
0 0.45 1 2 5.5
Sabemos que limx->+inff(x)=-inf.
Sabemos que f(1)=0, f(0)<0, f(0.45)>0 y f(5.5)>0.
Observando el signo de f', tenemos que f tiene una única raíz entre 0 y 0.45, y
una única raíz mayor que 5.5.
- 0 + + 0 + 0 -
sg f' |-----|-----|-----|-----|-----|----->
0 α 0.45 1 5.5 β
~ ~
α=0.15 y β=8.85.
|
|
|
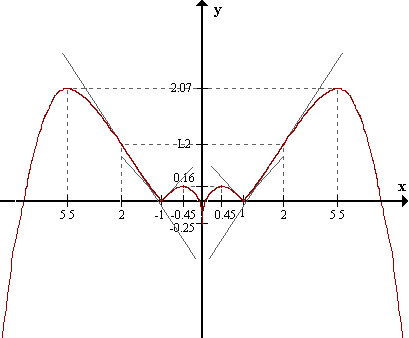
Máximo en (0.45,0.16).
Máximo en (5.35,2.07).
Punto anguloso en (1,0).
- Tangente por la derecha: y = (1/2)x - 1/2.
- Tangente por la izquierda: y = (-1/2)x + 1/2.
Punto de inflexión en (2,L2).
- Tangente: y = L2x - L2.
(La gráfica es simétrica con respecto al eje oy.)
|
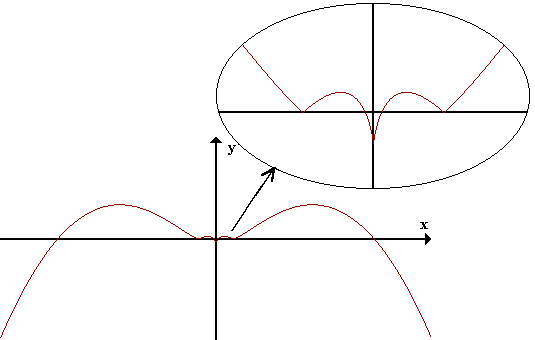
Para terminar, confirmemos nuestro análisis observando la gráfica exacta de la función:
<< anterior siguiente >>
|
|
Página principal
Tabla de Contenidos
Noticias matemáticas
|


