|
|
|
Estudio analítico y representación gráfica de:
2L|x| + 1 x
f(x) = --------- - ---
L|x| + 1 4e
Para conocer los detalles del procedimiento que seguiremos, ir a la página sobre
estudio analítico y representación gráfica de funciones.
Dominio
L|x| no está definido en x=0.
L|x| + 1 es 0 en x=1/e y x=-1/e, así que f no está definida en esos puntos.
Dominio de f: R - {0, 1/e, -1/e}
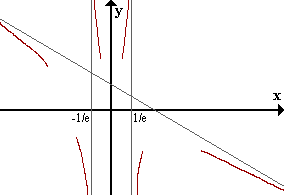
Continuidad y asíntotas verticales
0+/0-
-^-
2L|x| + 1 x
lim --------- - --- = 2
x->0+ L|x| + 1 4e
En x=0 discontinuidad evitable, f(0)=2
(-/+inf) 0+/0-
----^---- -^-
2L|x| + 1 x
lim --------- - --- = +inf AV: x=1/e
x->1/e+ L|x| + 1 4e
2L|x| + 1 x
lim --------- - --- = +inf AV: x=-1/e
x->-1/e+ L|x| + 1 4e
Ceros y signo
Pasaremos por alto este paso pues la ecuación f(x)=0 es difícil de resolver.
La expresión (2L|x| + 1)/(L|x| + 1) no es tan sencilla de graficar como para
aplicar el método de bacos.
Utilizaremos el método de Rolle para aproximar las raíces, luego de que contemos con
la información de los ceros y el signo de la derivada primera.
Asíntotas horizontales y oblicuas
2L|x| + 1 x
lim --------- - --- = +inf
x->+inf L|x| + 1 4e
2L|x| + 1 x
lim ----------- - --- = -1/4e
x->+inf x(L|x| + 1) x4e
2L|x| + 1 x x
lim --------- - --- + --- = 2 AO: y = (-1/4e)x + 2
x->+inf L|x| + 1 4e 4e
|
|
En x=0 discontinuidad evitable, f(0)=2.
AV: x=1/e y x=-1/e.
AO: y = (-1/4e)x + 2.
|
Derivada primera
2/x(L|x| + 1) - (2L|x| + 1)/x
f'(x) = ----------------------------- - 1/4e
(L|x| + 1)2
2L|x| + 2 - 2L|x| - 1 1
= --------------------- - 1/4e = ----------- - 1/4e
x(L|x| + 1)2 x(L|x| + 1)2
4e - x(L|x| + 1)2
= ------------------
4ex(L|x| + 1)2
Para determinar las raíces de la derivada primera emplearemos el
método de Rolle, luego de hallar la derivada segunda.
Derivada segunda
-((L|x| + 1)2 + x2(L|x| + 1)1/x)
f''(x) = -------------------------------- =
x2(L|x|+1)4
-(L|x|+1)(L|x|+1 + 2) -L|x|-3
= --------------------- = ----------
x2(L|x|+1)4 x2(L|x|+1)3
- E + 0 - E - 0 + E -
sg f'' -----|------|------|------|------|----->
-1/e -1/e3 0 1/e3 1/e
PI PI
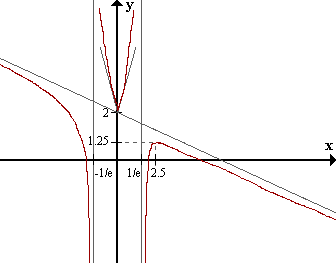
Puntos de inflexión: (-1/e3, 2.5) y (1/e3, 2.5).
Tangentes en los puntos de inflexión:
y = 4.93(x - 1/e3) + 2.5 = 4.93x + 2.25
y = -5.11(x + 1/e3) + 2.5 = -5.11x + 2.24
Ahora estudiaremos el signo de f'.
En primer lugar, determinaremos su signo en +infinito y -infinito.
1
lim ---------- - 1/4e = -1/4e
x->+inf x(L|x|+1)2
Luego determinamos su signo a derecha e izquierda de -1/e, 0 y 1/e.
1
lim ---------- - 1/4e = -inf
x->-1/e+ x(L|x|+1)2
1
lim ---------- - 1/4e = +inf
x->0+ x(L|x|+1)2
1
lim ---------- - 1/4e = +inf
x->1/e+ x(L|x|+1)2
También hallamos el signo de f' en -1/e3 y 1/e3:
f'(-1/e3)<0
f'(1/e3)>0
- E - - - E + + + E + 0 -
sg f' -----|-----|-----|-----|-----|-----|----->
-1/e -1/e3 0 1/e3 1/e α
Observando el signo de f'' vemos que f' decreciente para x mayores que 1/e, por lo tanto, tiene
en ese intervalo una única raíz α.
~
α = 2.5
~
f(2.5) = 1.25
f tiene un máximo en (2.5, 1.25)
f tiene un mínimo en (0,2)
|
|
Máximo en (2.5, 1.25).
Mínimo en (0,2).
Puntos de inflexión:
(-1/e3, 2.5)
- Tangente: -5.11x + 2.24
(1/e3, 2.5)
- Tangente: 4.93x + 2.25
|
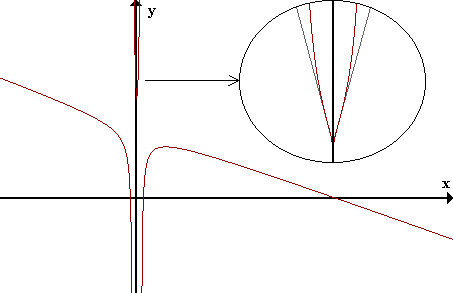
Finalmente, verifiquemos nuestro análisis observando la gráfica exacta de la función:
<< anterior
|
|
Página principal
Tabla de Contenidos
Noticias matemáticas
|


