|
|
|
Estudio analítico y representación gráfica de f(x) = L2|x| - (x-1)2/2.
Para conocer los detalles del procedimiento que seguiremos, ir a la página sobre
estudio analítico y representacion gráfica de funciones.
Dominio
L|x| no está definido en x=0.
Dominio de f: R - {0}
Continuidad y asíntotas verticales
lim L2|x| - (x-1)2/2 = +inf
x->0+
=> AV x=0
Ceros y signo
Pasaremos por alto este paso pues la ecuación f(x)=0 es difícil de resolver.
Las dos expresiones que aparecen (L2|x| y (x-1)2/2) no son tan sencillas
de graficar como para aplicar el método de Ábacos.
Utilizaremos el método de Rolle para aproximar las
raíces, luego de que contemos con la información de los ceros y el signo de
la derivada primera.
Asíntotas horizontales y oblicuas
lim L2|x| - (x-1)2/4 = -inf por órdenes de infinitos
x->+inf
0 +inf
---^--- ----^----
lim L2|x|/x - (x-1)2/2x = +inf
x->+inf
=> DA || oy para x->+inf y x->-inf.
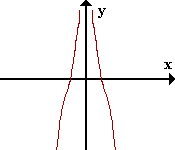
|
|
AV: x=0.
DA paralela al eje oy para -inf y +inf.
|
Derivada primera
1 2(x - 1) 2L|x| - (x2 - x) g(x)
f'(x) = 2L|x|--- - -------- = ---------------- = ---
x 2 x x
Para hallar el signo de g(x), aplicaremos el método de Ábacos:
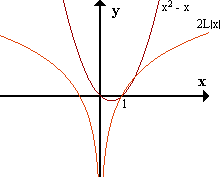
- E - 0 + 0 -
sg g(x) -----|-----|-----|----->
0 1 α
~
g(2) = -0.61
~
g(1.6) = -0.02 | ~
~ > α = 1.55
g(1.5) = 0.61 |
+ E - 0 + 0 -
sg f'(x) -----|-----|-----|----->
0 1 1.55
f(1) = 0
Mínimo en (1,0)
~
f(1.55) = 0.041
Máximo en (1.55, 0.04)
Ceros y signo
L|x| no existe en x=0, así que podemos marcar el 0 como un punto donde f no existe.
Sabemos por el estudio de asíntotas que la función tiende a -inf
cuando x->+inf y cuando x->-inf, así que ponemos un signo "-" en
los extremos del eje.
También sabemos que f tiende a +inf cuando x->0, así que ponemos un signo
"+" a la izquierda y a la derecha de 0.
- + E + -
sg f ----------|---------->
0
Observando el signo de f vemos hay al menos una raíz menor que 0, y al menos una raíz
mayor que 0.
El signo de f' es positivo para x<0, lo que indica que f es creciente en ese intervalo, por lo tanto
sólo tiene una raíz menor que 0, llamémosle α.
Sabemos que f tiene un mínimo en (1,0), así que 1 es una raíz de f, y el signo
de f es positivo a izquierda y derecha.
Luego del máximo en (1.55, 0.041), f es decreciente, así que hay una única raíz
después de 1.55, llamémosle β.
- 0 + E + 0 + 0 -
sg f -----|-----|-----|-----|----->
α 0 1 β
Mediante un proceso de aproximación, trataremos de descubrir α y β,
o acercarnos a ellas.
f(-1) = -2
f(-0.5) = -0.64
~
f(-0.4) = -0.14 | ~
~ > => α = -0.35
f(-0.3) = 0.6 |
~
f(2) = -0.02 | ~
~ > => β = 1.95
f(1.9) = 0.007 |
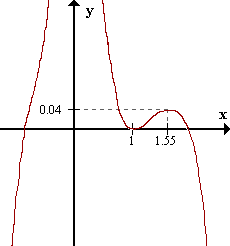
|
|
Mínimo en (1,0).
Máximo en (1.55, 0.04).
|
Derivada segunda
2.1/x.x - 2L|x| 2 - 2L|x|
f''(x) = --------------- - 1 = --------- - 1
x2 x2
-2L|x| - x2 + 2 h(x)
= -------------- = ----
x2 x2
Para hallar el signo de f''(x), aplicaremos el método de Ábacos
a h(x) = -2L|x| - (x2 - 2)
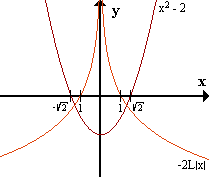
- - - 0 + + + E + + + 0 - - -
sg h -----|-----|-----|-----|-----|-----|-----|----->
_ _
-\|2 α -1 0 1 β \|2
h(-1.2) = 0.19 | ~
> => α = -1.25
h(-1.3) = -0.21 |
~
h es par, así que β = 1.25
- 0 + E + 0 -
sg f'' -----|-----|-----|----->
-1.25 0 1.25
PI PI
~
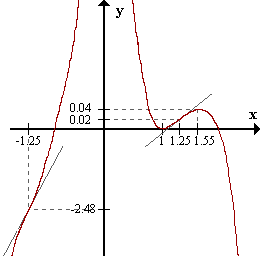
f(-1.25) = -2.48
f presenta un punto de inflexión en (-1.25, -2.48).
~
f'(-1.25) = 1.89
Tangente en el punto: y = 1.89(x + 1.25) - 2.48 = 1.89x - 0.12.
~
f(1.25) = 0.02
f presenta un punto de inflexión en (1.25, 0.02).
~
f'(1.25) = 0.1
Tangente en el punto: y = 0.1(x-1.25) + 0.02 = 0.1x - 0.10.
|
|
Punto de inflexión en (-1.25,-2.48)
- Tangente: y = 1.89x - 0.12
Punto de inflexión en (1.25,0.02)
- Tangente: y = 0.1x - 0.10
|
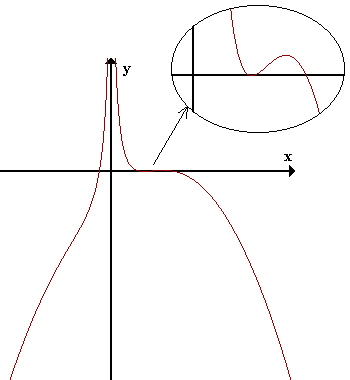
Finalmente, confirmemos nuestro estudio observando la gráfica precisa de la función:
<< anterior siguiente >>
|
|
Página principal
Tabla de Contenidos
Noticias matemáticas
|


