Es difícil, si no imposible, aprender un tema tan sólo leyéndolo, sin aplicar la información a problemas específicos que fuercen al lector a pensar en lo que ha leído. Además se aprenden mejor aquellas cosas que uno descubre por sí mismo.
Donald Knuth.
 

Infinitos

Definición

Infinito

f(x) es un infinito en a si limx->af(x) = inf

Ejemplo: limx->2 3/(x-2) = inf => 3/(x-2) es un infinito cuando x tiende a 2.

Infinitos fundamentales

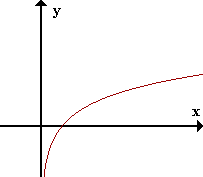
  1. Infinito logarítmico.
    limx->+inf Lx = +inf
    		 f(x) = Lx f(x)=Lx

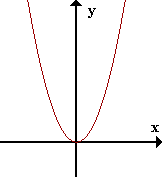
  2. Infinito potencial
    limx->+inf xn = +inf
    n natural, n≠0
    		 f(x)=x^2 f(x)=x2

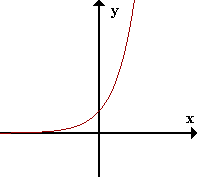
  3. Infinito exponencial
    limx->+inf ax = +inf
    a perteneciente a R+     		f(x)=e^x f(x)=ex

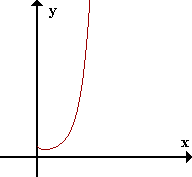
  4. Infinito potencial exponencial
    limx->+inf xnx = +inf
    n natural, n≠0
    		 f(x)=x^x f(x) = xx, x > 0

Definición

Infinitos equivalentes

Se dice que dos infinitos f(x) y g(x) son equivalentes si el limx->af(x)/g(x) = 1

limx->a f(x) = inf, limx->ag(x) = inf
f(x) es equivalente a g(x) <=> limx->af(x)/g(x) = 1

Comparación de infinitos

Sean f(x) y g(x) dos infinitos en a.
  1. Se dice que f(x) y g(x) tienen el mismo orden si limx->af(x)/g(x) = k ≠ 0
  2. Se dice que el orden de f(x) es mayor que el orden de g(x) si limx->af(x)/g(x) = inf
  3. Se dice que el orden de f(x) es menor que el orden de g(x) si limx->af(x)/g(x) = 0
  4. Cuando no existe limx->af(x)/g(x) se dice que los infinitos no son comparables.

Teorema

La suma de dos infinitos de distinto orden es equivalente al infinito de mayor orden.
H) f(x)x->a--> inf, g(x)x->a--> inf, orden(f(x)) < orden(g(x))
T) f(x) + g(x) equivalente a g(x) cuando x->a.

Demostración: 
                       1      0 pues orden (f(x)) < orden (g(x))
                     --^--  --^--   
    f(x) + g(x)       g(x)  f(x)     
lim ---------- = lim  --- + --- = 1 => f(x) + g(x) equiv g(x) 
x->a    g(x)     x->a g(x)  g(x)    |   x->a 
                                    |  
                                por def. de infinitos equivalentes

Comparación de infinitos fundamentales

orden Lx < orden xn < orden ax < orden xnx (x->+inf)

Ejemplo: limx->+inf Lx/x3= 0 pues orden Lx < orden x3 cuando x->+inf.

Teorema

Sustitución de infinitos equivalentes

H) limx->a α(x).f(x) = b (finito o infinito)
    α(x)x->a--> inf
    Existe β(x), β(x)x->a--> inf / β(x)x->a equiv α(x)
T) limx-a β(x).f(x) = b

Demostración: 
                                    pues lim α(x)/β(x) = 1
                                     |   x->a
                     α(x).β(x).f(x)  |         
lim α(x).f(x) = lim ---------------  = lim β(x).f(x) = b
x->a            x->a      β(x)         x->a

Ejemplo

             (ex + x2) equiv ex por comparación de 
                   |            infinitos fundamentales
               1   |          1             1
lim (ex + x2).---  =  lim  ex.---  =  lim   --- = 0
x->+inf       e2x     x->+inf e2x    x->+inf ex

Teorema

Sustitución de infinitos equivalentes

H) limx->a f(x)/α(x) = b (finito o infinito)
    α(x)x->a--> inf
    Existe β(x), β(x)x->a--> inf / β(x)x->a equiv α(x)
T) limx-a f(x)/β(x) = b

Demostración: 
                        pues lim β(x)/α(x) = 1
                          |  x->a
    f(x)       β(x).f(x)  |     f(x)        
lim ---- = lim ---------  = lim ---- = b
x->a α(x) x->a β(x).α(x)    x->a β(x)

<< anterior  siguiente >>

Página principal

Tabla de Contenidos

Noticias matemáticas
 
Cálculo > Límites
Límite finito – Teoremas – Límite infinito – Operaciones con límites – Límites de polinomios – Límites tipo – Infinitésimos – Infinitos – Cálculo de límites – Ejercicios

Última modificación: noviembre 2004
Página principal     Tabla de contenidos     E-mail